TensorFlow初心者でもGANを学習できた
今回は流行りのネタ，DeepなLearningをしてみます．とは言っても公式チュートリアルをなぞるだけでは恐らくその後何も作れないので，ちょっとは頭で考えながらコードを書いていきます．
この記事は，TensorFlowのチュートリアル通りにMNISTデータを学習できたものの，それが何をやっているか，或いはチュートリアルの次に進もうとしているが，自分でモデルを作成するためにどういう方針でコードを書いていくべきなのかが分からない読者を対象にしています．そう，私のことです．
TensorFlowチュートリアルの次にやるべきことは
私の場合，それはGANを自分の手で実装することでした．GANはモデルの概念は分かりやすいのでやるべきことは明確です．しかしCNNよりは複雑なので自ら実装するとなるとちゃんとTensorFlowを知らなくてはできないですし，学習結果が視覚的に分かりやすくモチベーションが高く保てるため，学習教材として最適だと考えました．
GANの実装
実装に際し，以下のgithubを特に実装の参考にしました．今回の実装はこれのほぼ写経です．
https://github.com/yihui-he/GAN-MNIST/tree/master/mnisthttps://www.tensorflow.org/tutorials/layers
また，理論や実装の考えなどは下記リンクを参考にしました．コード例がTensorFlowではなくKerasですが，それゆえに本質的な部分を理解するのに最適です．
GAN(DCGAN)とは
GANとは，「近年のDeep Learning研究の中で最もCoooooolなアイディア」とも評価されているDeep Neural Networkで，画像生成によく用いられます．以下，概念を簡単におさらいします．
GANは，Generator(以下G)とDiscriminator(以下D)という2つのネットワークから構成されます．Gはベクトルから画像を生成するネットワークで，Dは画像を入力するとそれがG由来（偽物）かデータセット由来（本物）かを判定するネットワークです．Gは出力画像を入力したDの出力がG由来と判定されないように，Dは逆にG由来の画像を正しくG由来だと判定できるように，相互に学習を進めていきます．勿論，学習の初期はGもノイズみたいな画像しか出さず，Dもガバガバな判定しか出しません．しかし学習が進むにつれてGもDも徐々に高度になっていき，最終的にはGからはデータセットと区別のつかない画像が出力されるようになる，という仕組みです．より詳しい説明は別のサイトでいっぱい紹介されていると思うので，そちらを参照してください．
「うん，アイディアは良く分かった．確かに上手くいくんだろう．でもこれどうやって実装すんの？俺にできる気がしない．．．」
というのが，チュートリアルを終えたばかりの人間の正直な感想でしょう．なので具体的に見てみます．
MNISTのためのGANモデル
MNISTは0~9の手書き数字が書かれた28x28のグレースケール画像ですので，Generatorの出力とDiscriminatorの入力は28x28x1次元の3階テンソルである必要があります．このGANの目的は，手書き数字っぽい画像を生成できるようにすることです．
Generator
乱数入力ベクトルから「手書き数字っぽい画像」を出力するモデルです．
100次元ベクトル -> [全結合] -> [バッチ正則化] -> [ReLU活性化] -> 1024次元ベクトル
1024次元ベクトル -> [全結合] -> [バッチ正則化] -> [ReLU活性化] -> [7x7画像化] -> 7x7x128画像
7x7x128画像 -> [5x5転置畳み込み, 2x2ストライド] -> [バッチ正則化] -> [ReLU活性化] -> 14x14x64画像
14x14x64画像 -> [5x5転置畳み込み，2x2ストライド] -> [バッチ正則化] -> [sigmoid活性化] -> 28x28x1画像
Generatorの入力ベクトルの次元は別に100次元である必要はないと思いますが，2層目，3層目，4層目で2x2のアップサンプリングがなされていくため，出力が28x28x1であれば自然と 7x7 -> 14x14 -> 28x28 と決まります．ここで2次元転置畳み込みとは，CNNにおける2次元畳み込みの逆操作に相当し，ある意味「逆畳み込み」のようなものですが，本質的には逆畳み込み(deconvolution)ではないらしいです．2次元転置畳み込みにおける2x2ストライドは，2x2 Up-Samplingに相当します．
この部分の定義に相当するコードは以下の通り．計算グラフを作成する段階の考え方はチュートリアルと何ら変わりません．自分で構築していくモデルなので，計算グラフが正しくつながっているか（結合係数の次元数の設定が適切か）は誰も保証しません．ここは特に注意する必要があります．
※後でGとDをまとめたDCGANクラスとして実装するので，ここで提示するコードは理解のための疑似コードとして読んでください（最後にソースコードをまとめて載せます）．
#不定の次元数の定義 dim_z=100, dim_W1=1024, dim_W2=128, dim_W3=64, dim_ch=1, # TensorFlow内学習係数の定義 ## Generator self.g_W1 = tf.Variable(tf.random_normal([dim_z, dim_W1], stddev=0.02), name="g_W1") self.g_b1 = tf.Variable(tf.random_normal([dim_W1], stddev=0.02), name="g_b1") self.g_W2 = tf.Variable(tf.random_normal([dim_W1, dim_W2*7*7], stddev=0.02), name="g_W2") self.g_b2 = tf.Variable(tf.random_normal([dim_W2*7*7], stddev=0.02), name="g_b2") self.g_W3 = tf.Variable(tf.random_normal([5, 5, dim_W3, dim_W2], stddev=0.02), name="g_W3") self.g_b3 = tf.Variable(tf.random_normal([dim_W3], stddev=0.02), name="g_b3") self.g_W4 = tf.Variable(tf.random_normal([5, 5, dim_ch, dim_W3], stddev=0.02), name="g_W4") self.g_b4 = tf.Variable(tf.random_normal([dim_ch], stddev=0.02), name="g_b4")
# Generaterの計算グラフ def generate(self, Z): # 1層目 fc1 = tf.matmul(Z, self.g_W1) + self.g_b1 bm1, bv1 = tf.nn.moments(fc1, axes=[0]) # バッチ平均，分散 bn1 = tf.nn.batch_normalization(fc1, bm1, bv1, None, None, 1e-5) relu1 = tf.nn.relu(bn1) # 2層目 fc2 = tf.matmul(relu1, self.g_W2) + self.g_b2 bm2, bv2 = tf.nn.moments(fc2, axes=[0]) bn2 = tf.nn.batch_normalization(fc2, bm2, bv2, None, None, 1e-5) relu2 = tf.nn.relu(bn2) # [batch, dim_W2*7*7] -> [batch, 7, 7, dim_W2] y2 = tf.reshape(relu2, [self.batch_size, 7,7,self.dim_W2]) # 3層目 conv_t1 = tf.nn.conv2d_transpose(y2, self.g_W3, strides=[1,2,2,1], output_shape=[self.batch_size, 14,14,self.dim_W3]) + self.g_b3 bm3,bv3 = tf.nn.moments(conv_t1, axes=[0, 1, 2]) bn3 = tf.nn.batch_normalization(conv_t1, bm3, bv3, None, None, 1e-5) relu3 = tf.nn.relu(bn3) # 4層目 conv_t2 = tf.nn.conv2d_transpose(relu3, self.g_W4, strides=[1,2,2,1], output_shape=[self.batch_size, 28, 28, self.dim_ch]) + self.g_b4 img = tf.nn.sigmoid(conv_t2) return img
Discriminator
Generatorの出力画像とデータセット画像とを見分けるように学習するモデルです．
28x28x1画像 -> [5x5畳み込み，2x2ストライド] -> [leaky ReLU活性化] -> 14x14x64画像
14x14x64画像 -> [5x5畳み込み，2x2ストライド] -> [leaky ReLU活性化] -> 7x7x128画像
7x7x128画像 -> [ベクトル化] -> [全結合, dropoutあり] -> [leaky ReLU活性化] -> [dropout] -> 256次元ベクトル
256次元ベクトル -> [全結合] -> [sigmoid活性化] -> 1次元ベクトル（判定確率）
こちらは 画像入力→ベクトル出力 という，TensorFlowチュートリアルでも組んだ覚えのあるモデルなので，そこまで理解に苦しむことはないでしょう．違いは出力層が1次元ベクトル（＝スカラー量）であることだけです．出力層が1の時はデータセット，0の時はGeneratorの出力と判定します．層が深いDNNの場合，全結合層の代わりにglobal average poolingを使うとよいとされています．ただしこれは収束が遅くなるため，今回のように浅い場合は全結合のままで構わないそうです．この部分に該当するコードは次の通り．
#不定の次元数の定義 dim_z=100, dim_W1=1024, dim_W2=128, dim_W3=64, dim_ch=1, # TensorFlow内学習係数の定義 ## Discriminator self.d_W1 = tf.Variable(tf.random_normal([5,5,dim_ch,dim_W3], stddev=0.02), name="d_W1") self.d_b1 = tf.Variable(tf.random_normal([dim_W3], stddev=0.02), name="d_b1") self.d_W2 = tf.Variable(tf.random_normal([5,5,dim_W3,dim_W2], stddev=0.02), name="d_W2") self.d_b2 = tf.Variable(tf.random_normal([dim_W2], stddev=0.02), name="d_b2") self.d_W3 = tf.Variable(tf.random_normal([dim_W2*7*7,dim_W1], stddev=0.02), name="d_W3") self.d_b3 = tf.Variable(tf.random_normal([dim_W1], stddev=0.02), name="d_b3") self.d_W4 = tf.Variable(tf.random_normal([dim_W1, 1], stddev=0.02), name="d_W4") self.d_b4 = tf.Variable(tf.random_normal([1], stddev=0.02), name="d_b4")
# Discriminaterの計算グラフ def discriminate(self, img): # 1層目 conv1 = tf.nn.conv2d(img, self.d_W1, strides=[1,2,2,1], padding="SAME") + self.d_b1 y1 = leaky_relu(conv1) # 2層目 conv2 = tf.nn.conv2d(y1, self.d_W2, strides=[1,2,2,1], padding="SAME") + self.d_b2 y2 = leaky_relu(conv2) # 3層目 vec, _ = tensor_to_vector(y2) fc1 = tf.matmul(vec, self.d_W3) + self.d_b3 y3 = leaky_relu(fc1) # 4層目 fc2 = tf.matmul(y3, self.d_W4) + self.d_b4 y4 = tf.nn.sigmoid(fc2) return y4
コスト関数
判定確率Dは0から1の値なので，対数を取ると の範囲をとります．これを利用して，確率の対数の負値を最小化することで確率を1に近づけます．
Gに入力される乱数ベクトルをとすると，
はGの出力がDによってデータセットの一部だと判定される確率です．Dには間違えてほしいので，
が望ましいです．従って，Gのコスト関数は次の式で表せます．
$$ J_G = {1 \over batch}\sum_{batch} {-log(D(G(z)))} $$
一方で，Dの目的はGの出力とデータセットを正しく見分ける事です．つまり，
でかつ
であることが望ましいです．このことをコスト関数を使って表すと次のようになります．
$$ J_D = {1 \over batch}\sum_{batch} {-log(1-D(G(z))) - log(D(x)) } $$
以上をまとめた計算グラフのソースコードは次のようになります．
# プレースホルダーの用意 Z = tf.placeholder(tf.float32, [self.batch_size, self.dim_z]) # Generatorへの入力 # 画像の用意 img_real = tf.placeholder(tf.float32, [self.batch_size]+self.image_shape) # Discriminatorへの入力 img_gen = self.generate(Z) # 出力 raw_real = self.discriminate(img_real) raw_gen = self.discriminate(img_gen) # 確率 p_real = tf.nn.sigmoid(raw_real) p_gen = tf.nn.sigmoid(raw_gen) # コスト関数の定義 discrim_cost = tf.reduce_mean( -tf.reduce_sum(tf.log(p_real) + \ tf.log(tf.ones(self.batch_size, tf.float32) - p_gen), axis=1)) gen_cost = tf.reduce_mean(-tf.reduce_sum(tf.log(p_gen), axis=1))
Dのコスト関数において，1の代わりにtf.ones(batch_size, tf.float32)を使用します．これは，コスト関数には1個の画像だけでなくまとまった量のバッチが流れてくるため，そのバッチサイズ分の1を用意する必要があるからです．
また，チュートリアルで組んだCNNとは異なり，G用とD用でコスト関数が2個になっています．ただしどちらのコスト関数でも互いのモデルを使用するため，Gを学習するときとDを学習するときでそれぞれのパラメータは共通でなければなりません．もしGとDを別々のクラスとして実装する場合は，この点に注意しましょう（うっかりD学習時とG学習時で別のインスタンスにしてしまうと，メンバ変数がそれぞれの学習で共有されず学習が進まないなんて事態も考えられます）．
学習の戦略
GとDの目的関数は相反する内容であるため，すべての変数をどちらの最適化でも考慮してしまうと学習が全く進みません．従って，Gの学習プロセスではGに関わる変数だけ，逆にDの学習プロセスではDの変数だけを最適化計算させなくてはなりません．さて，実は上のコードで，tf.Variable()に学習係数を登録する際にひっそりと名前(name=)を個別につけていました．
# Generator self.g_W2 = tf.Variable(tf.random_normal([dim_W1, dim_W2*7*7], stddev=0.02), name="g_W2") self.g_b2 = tf.Variable(tf.random_normal([dim_W2*7*7], stddev=0.02), name="g_b2") # Discriminator self.d_W2 = tf.Variable(tf.random_normal([5,5,dim_W3,dim_W2], stddev=0.02), name="d_W2") self.d_b2 = tf.Variable(tf.random_normal([dim_W2], stddev=0.02), name="d_b2")
この時，名前の添え字を見るだけでG用かD用か見分けられるようにしてありました．こうすることで，D用とG用それぞれの最適化メソッドにバインドする変数リストを簡単に与えられます．
# tensorflow変数の準備 discrim_vars = [x for x in tf.trainable_variables() if "d_" in x.name] gen_vars = [x for x in tf.trainable_variables() if "g_" in x.name] # 最適化メソッドの用意 optimizer_d = tf.train.AdamOptimizer(0.0002, beta1=0.5).minimize(d_cost_tf, var_list=discrim_vars) optimizer_g = tf.train.AdamOptimizer(0.0002, beta1=0.5).minimize(g_cost_tf, var_list=gen_vars)
GとDの2つのモデルは同時に（交互に）学習する必要があります．どちらから学習を始めても構いませんが，私は偶数番目をG，奇数番目をDの学習に充てました．バッチサイズ毎に最適化させるモデルを切り替えつつ，データセットからバッチを取り終わったら（1 epoch回ったら）またデータセットをシャッフルしてループを回す，というような方法になっています．
# 学習開始 itr = 0 # epoch毎のfor for epoch in range(n_epochs): index = np.arange(len(train_imgs)) np.random.shuffle(index) trX = train_imgs[index] # batch_size毎のfor for start, end in zip( range(0, len(trX), batch_size), range(batch_size, len(trX), batch_size)): # 画像は0-1に正規化 Xs = trX[start:end].reshape([-1, 28,28,1]) / 255. Zs = np.random.uniform(-1,1, size=[batch_size, dcgan_model.dim_z]).astype(np.float32) if np.mod(itr, 2) != 0 : # 偶数番目はGeneratorを学習 _, gen_loss_val = sess.run([optimizer_g, g_cost_tf], feed_dict={Z_tf:Zs}) discrim_loss_val, p_real_val, p_gen_val \ = sess.run([d_cost_tf, p_real, p_gen], feed_dict={Z_tf:Zs, image_tf:Xs}) #print("=========== updating G ==========") #print("iteration:", itr) #print("gen loss:", gen_loss_val) #print("discrim loss:", discrim_loss_val) else: # 奇数番目はDiscriminatorを学習 _, discrim_loss_val = sess.run([optimizer_d, d_cost_tf], feed_dict={Z_tf:Zs, image_tf:Xs}) gen_loss_val, p_real_val, p_gen_val = sess.run([g_cost_tf, p_real, p_gen], feed_dict={Z_tf:Zs, image_tf:Xs}) #print("=========== updating D ==========") #print("iteration:", itr) #print("gen loss:", gen_loss_val) #print("discrim loss:", discrim_loss_val) #print("Average P(real)=", p_real_val.mean()) #print("Average P(gen)=", p_gen_val.mean()) itr += 1
以上がTensorFlowで実装するGANのあらましです．
遭遇したエラー
ValueError: No gradients provided for any variable, check your graph for ops that do not support gradients, between variables
これは微分演算ができないことを示しています．理由は書き方のミスで，計算グラフがどこかで途絶えているからです．目を凝らして順々に計算グラフを追っていき，余計な変数や誤った変数に接続していないか，結合係数の次元数が適切かを確かめてみましょう．
The value of a feed cannot be a tf.Tensor object. Acceptable feed values include Python scalars, strings, lists, numpy ndarrays, or TensorHandles.
バッチをfeedさせるときにtf.Tensorオブジェクトに変換できなかったことを示します．.eval()メソッドを使うとうまくいくらしいです．
学習例
最初20epochくらいまではほぼ真っ暗だったので本当に学習できているか心配になりましたが，250epoch以上からかなりはっきりと数字が生成されました．CPUで計算するととんでもなく時間がかかるので，GPUが利用可能なTensorFlowを推奨します．私の環境の場合，8時間くらいかかって100epochだったのが，10分程度で500epochまで学習できるようになりました．
全ソースコード
Jupyter環境のブロックに分けています
# tensorflowのロード import tensorflow as tf import numpy as np
# MNISTデータのダウンロード from tensorflow.examples.tutorials.mnist import input_data mnist = input_data.read_data_sets("MNIST_data", one_hot=True)
# 補助関数の定義 # 1次元ベクトル化 def tensor_to_vector(input): shape = input.get_shape()[1:].as_list() dim = np.prod(shape) return tf.reshape(input, [-1, dim]), dim # leaky ReLU活性化関数 def leaky_relu(input): return tf.maximum(0.2*input, input)
# DCGANクラスの定義 class DCGAN(): def __init__( self, batch_size=100, image_shape=[28,28,1], dim_z=100, dim_W1=1024, dim_W2=128, dim_W3=64, dim_ch=1, ): # クラス内変数の初期化 self.batch_size = batch_size self.image_shape = image_shape self.dim_z = dim_z self.dim_W1 = dim_W1 self.dim_W2 = dim_W2 self.dim_W3 = dim_W3 self.dim_ch = dim_ch # TensorFlow内学習係数の定義 ## Generator self.g_W1 = tf.Variable(tf.random_normal([dim_z, dim_W1], stddev=0.02), name="g_W1") self.g_b1 = tf.Variable(tf.random_normal([dim_W1], stddev=0.02), name="g_b1") self.g_W2 = tf.Variable(tf.random_normal([dim_W1, dim_W2*7*7], stddev=0.02), name="g_W2") self.g_b2 = tf.Variable(tf.random_normal([dim_W2*7*7], stddev=0.02), name="g_b2") self.g_W3 = tf.Variable(tf.random_normal([5, 5, dim_W3, dim_W2], stddev=0.02), name="g_W3") self.g_b3 = tf.Variable(tf.random_normal([dim_W3], stddev=0.02), name="g_b3") self.g_W4 = tf.Variable(tf.random_normal([5, 5, dim_ch, dim_W3], stddev=0.02), name="g_W4") self.g_b4 = tf.Variable(tf.random_normal([dim_ch], stddev=0.02), name="g_b4") ## Discriminator self.d_W1 = tf.Variable(tf.random_normal([5,5,dim_ch,dim_W3], stddev=0.02), name="d_W1") self.d_b1 = tf.Variable(tf.random_normal([dim_W3], stddev=0.02), name="d_b1") self.d_W2 = tf.Variable(tf.random_normal([5,5,dim_W3,dim_W2], stddev=0.02), name="d_W2") self.d_b2 = tf.Variable(tf.random_normal([dim_W2], stddev=0.02), name="d_b2") self.d_W3 = tf.Variable(tf.random_normal([dim_W2*7*7,dim_W1], stddev=0.02), name="d_W3") self.d_b3 = tf.Variable(tf.random_normal([dim_W1], stddev=0.02), name="d_b3") self.d_W4 = tf.Variable(tf.random_normal([dim_W1, 1], stddev=0.02), name="d_W4") self.d_b4 = tf.Variable(tf.random_normal([1], stddev=0.02), name="d_b4") def build_model(self): # プレースホルダーの用意 Z = tf.placeholder(tf.float32, [self.batch_size, self.dim_z]) # Generatorへの入力 # 画像の用意 img_real = tf.placeholder(tf.float32, [self.batch_size]+self.image_shape) # Discriminatorへの入力 img_gen = self.generate(Z) # 出力 raw_real = self.discriminate(img_real) raw_gen = self.discriminate(img_gen) # 確率 p_real = tf.nn.sigmoid(raw_real) p_gen = tf.nn.sigmoid(raw_gen) # コスト関数の定義 discrim_cost = tf.reduce_mean( -tf.reduce_sum(tf.log(p_real) + \ tf.log(tf.ones(self.batch_size, tf.float32) - p_gen), axis=1)) gen_cost = tf.reduce_mean(-tf.reduce_sum(tf.log(p_gen), axis=1)) return Z, img_real, discrim_cost, gen_cost, p_real, p_gen def generate(self, Z): # 1層目 fc1 = tf.matmul(Z, self.g_W1) + self.g_b1 bm1, bv1 = tf.nn.moments(fc1, axes=[0]) bn1 = tf.nn.batch_normalization(fc1, bm1, bv1, None, None, 1e-5) relu1 = tf.nn.relu(bn1) # 2層目 fc2 = tf.matmul(relu1, self.g_W2) + self.g_b2 bm2, bv2 = tf.nn.moments(fc2, axes=[0]) bn2 = tf.nn.batch_normalization(fc2, bm2, bv2, None, None, 1e-5) relu2 = tf.nn.relu(bn2) # [batch, dim_W2*7*7] -> [batch, 7, 7, dim_W2] y2 = tf.reshape(relu2, [self.batch_size, 7,7,self.dim_W2]) # 3層目 conv_t1 = tf.nn.conv2d_transpose(y2, self.g_W3, strides=[1,2,2,1], output_shape=[self.batch_size, 14,14,self.dim_W3]) + self.g_b3 bm3,bv3 = tf.nn.moments(conv_t1, axes=[0, 1, 2]) bn3 = tf.nn.batch_normalization(conv_t1, bm3, bv3, None, None, 1e-5) relu3 = tf.nn.relu(bn3) # 4層目 conv_t2 = tf.nn.conv2d_transpose(relu3, self.g_W4, strides=[1,2,2,1], output_shape=[self.batch_size, 28, 28, self.dim_ch]) + self.g_b4 img = tf.nn.sigmoid(conv_t2) return img def discriminate(self, img): # 1層目 conv1 = tf.nn.conv2d(img, self.d_W1, strides=[1,2,2,1], padding="SAME") + self.d_b1 y1 = leaky_relu(conv1) # 2層目 conv2 = tf.nn.conv2d(y1, self.d_W2, strides=[1,2,2,1], padding="SAME") + self.d_b2 y2 = leaky_relu(conv2) # 3層目 vec, _ = tensor_to_vector(y2) fc1 = tf.matmul(vec, self.d_W3) + self.d_b3 y3 = leaky_relu(fc1) # 4層目 fc2 = tf.matmul(y3, self.d_W4) + self.d_b4 #y4 = tf.nn.sigmoid(fc2) return fc2 def generate_samples(self, batch_size): # ここでは指定したbatch_sizeでサンプルを生成するため，self.batch_sizeは使わない Z = tf.placeholder(tf.float32, [batch_size, self.dim_z]) # 1層目 fc1 = tf.matmul(Z, self.g_W1) + self.g_b1 bm1, bv1 = tf.nn.moments(fc1, axes=[0]) bn1 = tf.nn.batch_normalization(fc1, bm1, bv1, None, None, 1e-5) relu1 = tf.nn.relu(bn1) # 2層目 fc2 = tf.matmul(relu1, self.g_W2) + self.g_b2 bm2, bv2 = tf.nn.moments(fc2, axes=[0]) bn2 = tf.nn.batch_normalization(fc2, bm2, bv2, None, None, 1e-5) relu2 = tf.nn.relu(bn2) # [batch, dim_W2*7*7] -> [batch, 7, 7, dim_W2] y2 = tf.reshape(relu2, [batch_size, 7,7,self.dim_W2]) # 3層目 conv_t1 = tf.nn.conv2d_transpose(y2, self.g_W3, strides=[1,2,2,1], output_shape=[batch_size, 14,14,self.dim_W3]) + self.g_b3 bm3,bv3 = tf.nn.moments(conv_t1, axes=[0, 1, 2]) bn3 = tf.nn.batch_normalization(conv_t1, bm3, bv3, None, None, 1e-5) relu3 = tf.nn.relu(bn3) # 4層目 conv_t2 = tf.nn.conv2d_transpose(relu3, self.g_W4, strides=[1,2,2,1], output_shape=[batch_size, 28, 28, self.dim_ch]) + self.g_b4 img = tf.nn.sigmoid(conv_t2) return Z, img
# モデルの構築 dcgan_model = DCGAN(batch_size=128, image_shape=[28,28,1]) Z_tf, image_tf, d_cost_tf, g_cost_tf, p_real, p_gen = dcgan_model.build_model() Z_gen, image_gen = dcgan_model.generate_samples(batch_size=32)
# セッション開始 sess = tf.InteractiveSession() saver = tf.train.Saver(max_to_keep=10)
# tensorflow変数の準備 discrim_vars = [x for x in tf.trainable_variables() if "d_" in x.name] gen_vars = [x for x in tf.trainable_variables() if "g_" in x.name] # 最適化メソッドの用意 optimizer_d = tf.train.AdamOptimizer(0.0002, beta1=0.5).minimize(d_cost_tf, var_list=discrim_vars) optimizer_g = tf.train.AdamOptimizer(0.0002, beta1=0.5).minimize(g_cost_tf, var_list=gen_vars)
# TensorFlow内のグローバル変数の初期化
tf.global_variables_initializer().run()
from matplotlib import pyplot as plt # 生成画像の可視化 def visualize(images, num_itr, rows, cols): # タイトル表示 plt.title(num_itr, color="red") for index, data in enumerate(images): # 画像データはrows * colsの行列上に配置 plt.subplot(rows, cols, index + 1) # 軸表示は無効 plt.axis("off") # データをグレースケール画像として表示 plt.imshow(data.reshape(28,28), cmap="gray", interpolation="nearest") plt.show()
# 学習 def train(train_imgs, n_epochs, batch_size): itr = 0 for epoch in range(n_epochs): index = np.arange(len(train_imgs)) np.random.shuffle(index) trX = train_imgs[index] # batch_size毎のfor for start, end in zip( range(0, len(trX), batch_size), range(batch_size, len(trX), batch_size)): # 画像は0-1に正規化 Xs = trX[start:end].reshape([-1, 28,28,1]) / 255. Zs = np.random.uniform(-1,1, size=[batch_size, dcgan_model.dim_z]).astype(np.float32) if np.mod(itr, 2) != 0 : # 偶数番目はGeneratorを学習 _, gen_loss_val = sess.run([optimizer_g, g_cost_tf], feed_dict={Z_tf:Zs}) discrim_loss_val, p_real_val, p_gen_val \ = sess.run([d_cost_tf, p_real, p_gen], feed_dict={Z_tf:Zs, image_tf:Xs}) #print("=========== updating G ==========") #print("iteration:", itr) #print("gen loss:", gen_loss_val) #print("discrim loss:", discrim_loss_val) else: # 奇数番目はDiscriminatorを学習 _, discrim_loss_val = sess.run([optimizer_d, d_cost_tf], feed_dict={Z_tf:Zs, image_tf:Xs}) gen_loss_val, p_real_val, p_gen_val = sess.run([g_cost_tf, p_real, p_gen], feed_dict={Z_tf:Zs, image_tf:Xs}) #print("=========== updating D ==========") #print("iteration:", itr) #print("gen loss:", gen_loss_val) #print("discrim loss:", discrim_loss_val) #print("Average P(real)=", p_real_val.mean()) #print("Average P(gen)=", p_gen_val.mean()) itr += 1 # サンプルを表示 z = np.random.uniform(-1,1, size=[32, dcgan_model.dim_z]).astype(np.float32) generated_samples = sess.run([image_gen], feed_dict={Z_gen:z}) #plt.imshow(generated_samples[0][0].reshape(28,28), cmap="gray", interpolation="nearest") visualize(generated_samples[0], epoch, 4,8) print("epoch = ", epoch)
train(mnist.test.images, 500, 128)
すっごくわかりにくい「明るさ」のはなし 〜Aqoursを添えて〜
だいぶご無沙汰していましたが，今回は私の専門の一つである色彩科学に関する話をしたいと思います．今回は明るさ，あるいは明暗，あるいは光の量を表す単位について，測光学の観点からできるだけ正確に書くことを試みます．
以下の文章は私が自分の知識の整理のために書くものです．よって厳密な正確性は保証しません（大学のレポートで使って×をつけられても知らないゾ！）．まだ不勉強な部分も多々ありますので，もし違っていたらご指摘お願いします．
あと，おたく特有の表現が出てきます．
その前に
光の明るさや明暗を表す用語は様々で，それぞれに微妙な違いがあります．例えば「輝度(luminance)」「照度(illuminance)」「明度(lightness)」「明るさ(brightness)」というのはそれぞれ明暗の違いを表す専門用語ですが，厳密にはこれらは全て違う概念です．以下ではこの違いについても詳しく触れていきます．従ってここでは，一般的な意味での明るさという表現を「明暗」と呼ぶことにします．
前提知識としては，電磁波の強度がエネルギー[W]で表せることを知っておけばいいでしょう．
明暗を定量的に取り扱うには
明暗は何から生じるでしょうか？光ですよね．光とは何でしょうか？電磁波です．では電磁波の強さを物理的に定量化すれば明暗の強さを定義できそうな気がしますよね？
ぶっぶー！ですわ！
これがやりたかった
考えてみてください．X線がいくら強かろうが，赤外線がいくら放射されてようが，携帯から無線の電波がいくら屋内を飛び回っていようが，明暗感覚には全く影響しません．ヒトが眼で感じられる光の範囲は決まっていて，およそ380nm~780nmの波長範囲の電磁波です．この範囲の光のことを「可視光」と呼びます．
「わかった！じゃあ可視光範囲だけ考えることにしよう！」
「悪くありませんわね．」
「確か光には線型性があるから，積分で表せる...だったよね？」
「その通りですわ！千歌さんにしては賢いですわね．」
「可視光範囲の単位時間あたりの放射エネルギー密度 [
]，なんて...どうかな？」
「式にすると？」
「をその光の波長
における放射エネルギー密度分布[
]として...こうだ！」
ぶっぶー！ですわ！
千歌ちゃんがなぜ怒られたのかというと，波長（色）による明暗の違いを全く考慮に入れてないからです．可視光の単色光，かつ同じ放射エネルギー密度であっても，ヒトにとっての明暗の感じられ方は大きく異なります．直感的にも，一般に青は暗くて黄色は明るく見える，というのは納得ですよね（この説明はちょっと厳密性に欠けますが）．これを表したのが分光視感効率と呼ばれるものです．（（2018/2/20追記）以降，単に「光」といった場合，分光視感効率を考慮した可視光を意味します．）
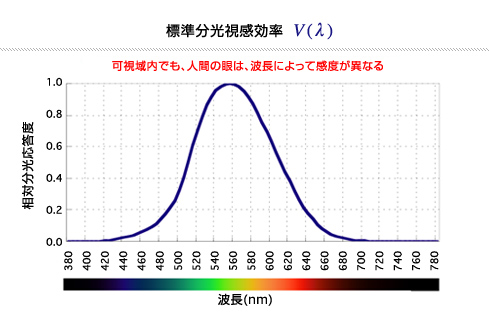
このグラフは，物理的に同じエネルギーを持った単色光が，ある波長の時にどれだけの明暗量（正確には輝度）としてヒトに知覚されるかを相対的に表したものです．例えばこのグラフから，480nmの単色光は560nmの単色光よりも約0.1倍明るく見える（＝10倍暗く見える），ということが読み取れます．
ちなみに分光視感効率をどうやって測定するかというと，フリッカーフォトメトリー(Flicker Photometry，交照法)と呼ばれる心理物理実験を使います．被験者に2種類の単色光をチカチカと素早く点滅させた光（フリッカー）を見せて「チラつきが見えなくなるように」一方の単色光の強度を調節してもらいます．チラつきは明暗に差があるときに生じると考えられるため，チラつきが無い＝明暗に差が無いと考えることで，相対的な明暗感覚の効率を波長分布として求めることができます．
ここまでで大事なことは，明暗量は物理量だけでなくヒトの心理特性まで考慮しないと定義できない量（心理物理量）であるということです．明暗を表す単位の一つ「カンデラ[cd]」が，SI基本単位の中で唯一，物理的に定義されていないのはこれが理由です．
※実は音の心理的な大きさを表すラウドネス[phon]も心理物理量であり，物理的に同じ音圧[Pa]であっても周波数毎に異なる量です．が，なぜかこちらは基本SI単位には含まれてません．
様々な明暗量の定義
輝度(Luminance)
上記の分光視感効率を用いて定義した，ある一点における明暗の量のことを「輝度」と呼びます．単位はカンデラ毎平方メートルあるいはニト
で，計算式は次の通りです．
このように輝度は積分で定義されるため，線型性が成り立ちます．これはつまり，異なる分光分布を持つ光源でさえも，輝度に対しては足し算や平均をしてよいことを意味します．
輝度は一般に，発光面（例えばディスプレイモニタ）の局所的な明暗を表す量として広く使われています．例えば，一般的なPCモニタの白色(255,255,255)は大体数百です．
ちなみに，たまに輝度のことをBrightnessという人たちもいますが，測光学的には厳密には間違いです．
※訂正(2018/2/20)：輝度の単位を間違えていたので修正．
光度(Luminous intensity)
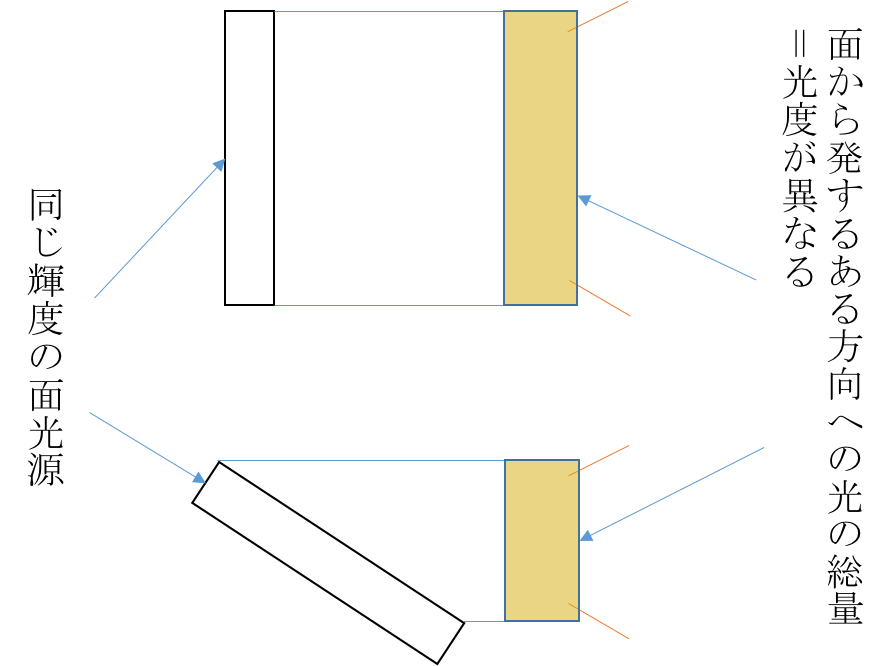
さて，輝度の単位を見るととついていますので，面積で積分してみたくなりますよね？すると，ある大きさを持った面光源，あるいは完全拡散反射面全体としての明暗量を与えることになります．これを「光度」と呼びます．単位はカンデラ[cd]です．光度はある方向から見た面全体としての明暗を表す量なので，例えば面を傾けて見た場合，輝度は減りませんが光度は減ります．光度は一般に，光源の面積を考える意味のないもの（例えば星）の明暗を表す時に使います．点みたいな星の見かけの面積で微分したら無限大の輝度になるし．
ちなみに，一般的なロウソクの火はおよそ1cdです．これは元々，光度の単位の定義にロウソクの火を用いていたことと関係します．
光束(Luminous flux)
光束という言葉は聞いたことがなくても，その単位「ルーメン[lm] = [cd str]」というのは，照明を買う時に気にしたことがあるかもしれません．光束とは，点光源から発生する，明暗を決める光の量そのものを表す量です．
「...ということですのよ！皆さん，分かりましたか？」
「いやぁ...だって光の量は光度ってさっき言ってなかったっけ？」
「光束と光度で何が違うの？ダイヤの言ってること良く分かりマセーン！」
「えっ...と...それは...」
では例えば，２種類の配光特性の異なる点光源を考えてみましょう．これらを同じ面積の孔から覗いてみます．
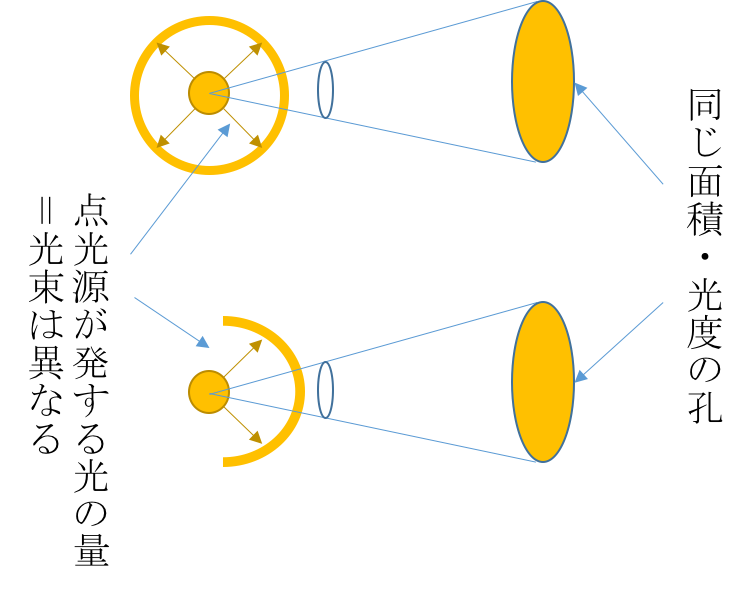
このとき，孔の光度（面全体で均一ならば輝度）が等しかったとします．しかし，光源A（上）はあらゆる方向に光を発する一方で，光源B（下）はある方向にしか光を出しません．孔を通過する光の量は確かに同じと言えますが，光源Aと光源Bは果たして全体として同じ量の光を放射していると言えるでしょうか？このような光の量の違いを表すのが，光束という量です．
点光源からは３次元的にあらゆる方向へ光が発せられるので，光束を計算するには２次元的な角度ではなく立体角で考えます．ですので，点光源から発せられるある面積を通過する光束
は，
が張る立体角
の積分として定義されます．
逆に言えば，光度は光束の立体角密度とも言えます．つまり，同じ光束の光源であっても鏡などで指向性を持たせてやれば，その方向においては光束の密度すなわち光度が大きくなります．懐中電灯とか豆電球のくせにやけに明るいですよね．
ちなみに，つまり点光源を囲む球面を考えた場合の光束のことを全光束と呼びます．全光束は点光源からあらゆる方向に発せられる光全てをカウントした量ですので，光源そのものの発光能力を示しているといえます．これが照明の能力を示す指標として全光束[lm]が使われる理由です．
照度(Illuminance)
一方で，光源や面で反射する光ではなく，光に照らされている対象の立場で考えた時の明暗を表す量も考えるべきです．同じ全光束の光源で照らしていても，その光源があまりにも遠い場所では暗いですよね．そのような明暗を表す量が照度で，単位はルクス[lx]=です．
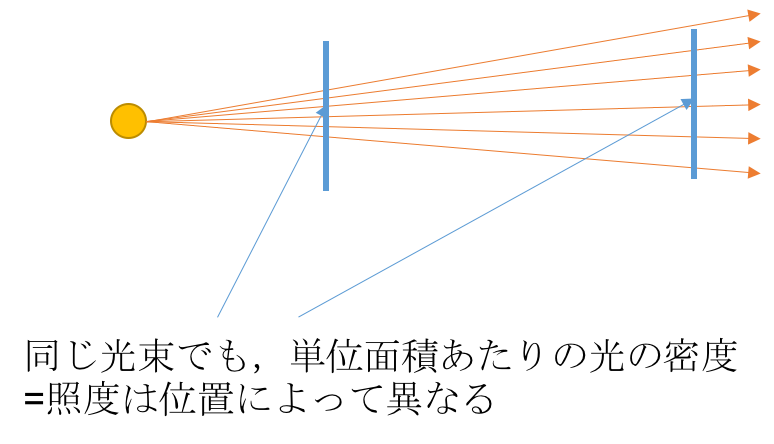
電気力線と同じく，光束は光線として考えることができます．点光源から離れれば離れるほど，同じ面積を通過する光線の数は減っていきます．これが照らされた時の明暗すなわち照度に相当します．従って定義式は次のようになります：
「うぇ，またなんか変な式が出てきたぁ！はっ，これぞもしや光と闇の魔術の真髄…！」
「いや，ある意味間違ってないけどむしろ初歩だから...」
「リリーには解ってしまうのね...この魔界から誘わんとする冥府の囁きが...」
「違うから！っていうか，光度や輝度と照度って何が違うのかしら？」
ある方向から出て行く単位立体角あたりの光線数（光束）が光度です．立体角は距離によって変わりませんので，光源から遠ざけてもその方向の光度は変わりません．一方で照度は単位面積あたりの光線数（光束）ですので，上で書いたように照度は光源から遠ざけると小さくなります．
均一な面光源の場合には輝度を考えます．この場合，光源の輝度は距離によって変化しません．しかし，このような面光源で照らした時の照度は光源からの距離によって変わり，照らされた面の反射光の輝度もまた変化します．実は，照らされている面の照度と，その面の反射光の輝度には次の関係式が成立します．
ここでは面の反射率です．証明は簡単なので飛ばします．このように，照度は反射面上に降り注ぐ光の明暗を表し，輝度は発光面あるいは反射面を見る時の明暗を表します．ここら辺，かなり分かりにくいと思いますが，よく読むと分かるはずです．
（2018/2/20追記）ちなみに，一般的なオフィスの照明設置条件では500~1000lxくらい，曇りの日の外だと数万lx，直射日光下だと大体10万lxくらいあります．太陽って凄まじい照度ですね．まぁ，真に凄いのはそんな幅広い照度範囲でも正常に機能する人間の眼の順応能力なのかも知れませんが...．
輝度は「明るさ」なのか？
さて，ここからは反射面の明暗のみについて議論していきます．これまで紹介した中で使えそうな用語は「輝度」ですが，果たして輝度は直感的な意味での「明るさ」と本当に対応しているのでしょうか？
例えばスマートフォン．明るさ調節機能を切った場合にはスマホの輝度は一定に保たれるはずです．この状態では勿論，まともに使えませんよね．屋外に出れば画面が暗すぎるし，寝る前に電気を消して画面を見ると明るすぎる，なんてことになります．つまり我々は，直感的な意味で「面の明るさ」と言った場合に，無意識的にその空間から見た相対的な明暗を判断しています．
また一方で，明るさ知覚量は輝度に比例しないことが知られています．すなわち，100と200
の差と,1000
と1100
の差は同じ明るさの差ではないのです．このことからも，輝度をそのまま明るさの単位とすることはできなさそう，ということがわかります．
「うーん…確かにスマホの明るさは違うね…」
「輝度と明るさが違うとなると，明るさってなんだろう？数値化できるのかな？」
「難しい問題ですわね…」
明度(Lightness)
少なくとも物体表面の明暗知覚については，ある程度数値化が試みられています．それはメイド明度と呼ばれています．計算式は以下の通り．
(if
)
(othewise)
ここでは物体表面の反射光の輝度，
はその環境下における完全拡散反射面（＝白色点，白色標準）の輝度を表します．上式から明度は，その環境下で反射面としてありうる最大輝度で正規化した反射光輝度の非線形出力として与えられることがわかります．これによって上で述べた「明るさの相対評価という特性」「輝度と明るさの非線形性」の2点をクリアしています．正規化しているため単位はありませんが，0~100の値をとるので，強いていうなら%でしょうか．
これはマンセル表色系という，色票の色を明度・色相・彩度の3要素で表現し，かつ知覚的に等間隔になるように定量的に表した表色系をもとに構成（近似）されています．マンセル値は色票固有の値なので，明度も色票固有です．上式で得られる明度は，反射面が定まれば照明によらず一意に定まります．
明るさ(Brightness)
物体表面に限って言えば，明るさはほぼ明度と対応します．ただし，明度と明るさは厳密には異なります．
「…って本に書いてあったずら．」
「お姉ちゃん，これって一体どういう事なの？」
「さあ，洗いざらい吐いてもらうわよっ！」
「ピギャアアアアアアアア！！知りませんわあああああ！！」
明度は物体表面に関する明暗知覚を表すので，厳密には発光面に対しては適用できません（ただしモニタの最大輝度を白色点として，擬似的に明度を求めることはできます）．対して明るさは，表面以外にも定義されうる量です．しかし，CIE（国際照明委員会）で「明るさ(brightness)」を表す心理物理量は現状採択されていません（2018/2/20追記：輝度とBrightnessの関係を測定している論文はありますが，有彩色光まで含めて明るさの関数を求めた例は私は知りません）．
他にも，照度を大きくすると，（表面自体が変わるわけではないので）明度は変わりませんが，明るさは変化します．相対的な量としても，白はより明るく（明度が高くなったように），黒はより暗く（明度が低くなったように）見えるようになります（スティーブンス効果）．また，明度の式からいえば，同じ照度下で同じ輝度ならば同じ明度になります．しかし実際には，そのような条件下で彩度の異なる色光・色票を観察した場合，高彩度の方がより明るく見えることが知られています（ヘルムホルツ-コールラウシュ効果）．更に最新の研究では，錐体の応答量だけでは明るさ知覚を説明できず，別の視細胞も関わっているのでは，なんて話も浮上しつつあります．
以上のように，「明るさ」と一言で言っても，そこには絶対的な明るさ（輝度と対応）と相対的な明るさ（明度と対応）が混在しています．そしてそのどちらについても，明るさを正確に表す式は今の所存在しません．実は明るさ知覚については今のところまだ解っていないことが多く，皆が納得できる形で定量化しきれていないのが現状です．
まとめ
ここまでに，心理物理量としての輝度，光度，光束，照度の定義，考え方と，それらの違いを説明しました．更に，輝度，明度，明るさは似た概念でありながら互いに完全には一致しないことを解説しました．特に明るさについては，現在は未だ完全な数値化ができていない量であることを述べました．
「…というわけで，明るさの話はこれでおしまいです．ルビィ，わかりましたか？」
「うん，複雑な話だったけどお姉ちゃんのお陰でよく分かったよ！」
「んまああああ！！流石私の妹！かわいいでちゅね〜よくできまちた〜」
「何これ…」
「さぁ…」
「明るさの話だけに2人共シャイニー☆ってことね！」
お粗末．
RealSenseをOpenCVで使う
今回紹介するクラスによって，RealSenseでVR or ARを実現するために必要なRealSenseの機能を簡単に使えるようになります．具体的には，
- RGBカメラ・デプスカメラ画像の取得
- デプスマップをRGBカメラから見た画像（とその逆）の取得
- デプスカメラを原点とする座標系（=RealSenseのワールド座標系）でのXYZ頂点座標の取得
- カメラ内部・外部パラメータ（デプスカメラから見たRGBカメラの位置姿勢）を取得
- 自動露出，自動ホワイトバランスの有効化・無効化
が可能となります．RGBカメラとデプスカメラは空間的に位置がずれているので，ARに使うためには外部パラメータが不可欠です．また，色に関する処理をする場合は自動露出がかえって邪魔になることがあるので，こちらも切れるようにしました．データはすべてOpenCVのcv::Matもしくはstd::vector<cv::Point3d>で取得できます．なお，カメラ内部パラメータはOpenCVで使える形式にしています．
サンプル
こんな感じに使います．
#include "RealSenseCVWrapper.h" int main(void) { RealSenseCVWrapper rscv(640, 480); rscv.getCalibrationStatus(); std::cout << "calibration data: " << "\n camera matrix = \n" << rscv.cameraMatrix << "\n camera distortion params = \n" << rscv.distCoeffs << "\n transform matrix of RGB cam = \n" << rscv.transform << std::endl; while (1) { cv::Mat src; // RealSenseのストリームを開始 rscv.queryFrames(); //rscv.getColorBuffer(src); // デプス画像にマップしたカラー画像を取得 rscv.getMappedColorBuffer(src); // 頂点座標の勾配を推定して陰影表示 rscv.getXYZBuffer(); cv::Mat XYZImage(rscv.bufferSize, CV_32FC1); for (int i = 1; i < rscv.bufferSize.height-1; i++) { for (int j = 1; j < rscv.bufferSize.width-1; j++) { // 隣4隅への勾配ベクトルを算出 float intensity = 0.0f; cv::Point3f v0, v1, v2, v3, v4; v0 = rscv.xyzBuffer[i*rscv.bufferSize.width + j]; if (v0.z != 0) { v1 = rscv.xyzBuffer[(i - 1)*rscv.bufferSize.width + (j - 1)] - v0; v2 = rscv.xyzBuffer[(i - 1)*rscv.bufferSize.width + (j + 1)] - v0; v3 = rscv.xyzBuffer[(i + 1)*rscv.bufferSize.width + (j + 1)] - v0; v4 = rscv.xyzBuffer[(i + 1)*rscv.bufferSize.width + (j - 1)] - v0; // それぞれの勾配から法線ベクトルを4種類算出して平均 // v1 v2 // v0 // v4 v3 // 法線方向は手前側が正 cv::Point3f n0, n1, n2, n3, n4; n1 = v2.cross(v1); n2 = v3.cross(v2); n3 = v4.cross(v3); n4 = v1.cross(v4); n0 = (n1 + n2 + n3 + n4) / cv::norm(n1 + n2 + n3 + n4); cv::Point3f light(3.f, 3.f, 0.f); intensity = n0.ddot(light/cv::norm(light)); } else { intensity = 0.f; } XYZImage.at<float>(i, j) = intensity; } } // RealSenseのストリームを終了 rscv.releaseFrames(); cv::imshow("ts", src); cv::imshow("xyz", XYZImage); int c = cv::waitKey(10); if (c == 27) break; if (c == 'a') { rscv.useAutoAdjust(false); rscv.setExposure(-8); rscv.setWhiteBalance(6000); } if (c == 'A') { rscv.useAutoAdjust(true); } } return 0; }
RealSenseCVWrapperクラスを初期化するには引数を指定する必要があります．あんまりC++の知識がないのでよくない実装な気もしますが，とりあえず動いているのでよしとしましょう．また，RealSenseCVWrapper::getXxxxBuffer()を利用する前と後をqueryFrames()とreleaseFrames()で挟む必要があります．デストラクタで終了処理をしているので，終了時については特に気にする必要はないと思います．
結果は次の画像のようになります．デプスカメラから見たカラー画像も，コマンド一つで取得可能です．また，XYZ座標値を可視化するために，法線を算出して簡単な拡散反射モデルで表示しています．
ソースコード
今回のクラスのソースコードです．自己責任でご利用ください．
RealSenseCVWrapper.h
#pragma once #include <opencv2\opencv.hpp> #include <RealSense\SenseManager.h> #include <RealSense\SampleReader.h> #pragma comment(lib, "libpxc.lib") class RealSenseCVWrapper { public: // constructor // @param // width : width of picture size // height: height of picture size RealSenseCVWrapper(); RealSenseCVWrapper(int width, int height); ~RealSenseCVWrapper(); void safeRelease(); // query RealSense frames // you should execute queryStream() function before get buffers // and releaseFrames(); function after all by every frame // @return // true = frame is succcessfully queried bool queryFrames(); void releaseFrames(); // get camera buffers void getColorBuffer(); void getDepthBuffer(); void getMappedDepthBuffer(); void getMappedColorBuffer(); void getXYZBuffer(); void getColorBuffer(cv::Mat &color); void getDepthBuffer(cv::Mat &depth); void getMappedDepthBuffer(cv::Mat &mappedDepth); void getMappedColorBuffer(cv::Mat &mappedColor); void getXYZBuffer(std::vector<cv::Point3f> xyz); // adjust camera settings // @param // use_aa: flag to use auto exposure and auto white balance void useAutoAdjust(bool use_aa); // set RGB camera exposure // @param // value: exposure time = 2 ^ value [s] // if you want 30fps you should set under 33 ~ 2 ^ -5 [ms] void setExposure(int32_t value); // set RGB camera white balance // @param // value: white point = value [K] // (ex: D65 standard light source = about 6500[K]) void setWhiteBalance(int32_t value); // get calibration status // - camera matrix // - distortion parameters // - transform matrix (RGB camera origin to depth camera origin) void getCalibrationStatus(); // OpenCV image buffer cv::Size bufferSize; // buffer size cv::Mat colorBuffer; // RGB camera buffer (BGR, 8UC3) cv::Mat depthBuffer; // depth camera buffer (Gray, 32FC1) cv::Mat colorBufferMapped; // RGB camera buffer mapped to depth camera (BGR, 8UC3) cv::Mat depthBufferMapped; // depth camera buffer mapped to RGB camera (Gray, 32FC1) std::vector<cv::Point3f> xyzBuffer; // XYZ point cloud buffer from depth camera (XYZ) // RGB camera calibration data writtern by OpenCV camera model cv::Mat cameraMatrix; // inclueds fx,fy,cx,cy cv::Mat distCoeffs; // k1,k2,p1,p2,k3 cv::Mat transform; // 4x4 coordinate transformation from RGB camera origin to the world (=depth) system origin protected: Intel::RealSense::SenseManager *rsm; Intel::RealSense::Sample *sample; };
RealSenseCVWrapper.cpp
(修正1/23)getColorBuffer()の問題を修正
#include "RealSenseCVWrapper.h" using namespace Intel::RealSense; using namespace cv; using namespace std; RealSenseCVWrapper::RealSenseCVWrapper() { } RealSenseCVWrapper::RealSenseCVWrapper(int w = 640, int h = 480) { rsm = SenseManager::CreateInstance(); if (!rsm) { cout << "Unable to create SenseManager" << endl; } // RealSense settings rsm->EnableStream(Capture::STREAM_TYPE_COLOR, w, h); rsm->EnableStream(Capture::STREAM_TYPE_DEPTH, w, h); if (rsm->Init() < Status::STATUS_NO_ERROR) { cout << "Unable to initialize SenseManager" << endl; } bufferSize = Size(w, h); } RealSenseCVWrapper::~RealSenseCVWrapper() { safeRelease(); } void RealSenseCVWrapper::safeRelease() { if (rsm) { //rsm->Release(); rsm->Close(); } } bool RealSenseCVWrapper::queryFrames() { if (rsm->AcquireFrame(true) < Status::STATUS_NO_ERROR) { return false; } sample = rsm->QuerySample(); } void RealSenseCVWrapper::releaseFrames() { rsm->ReleaseFrame(); } void RealSenseCVWrapper::getColorBuffer() { // Acquire access to image data Image *img_c = sample->color; Image::ImageData data_c; img_c->AcquireAccess(Image::ACCESS_READ_WRITE, Image::PIXEL_FORMAT_BGR, &data_c); // create OpenCV Mat from Image::ImageInfo Image::ImageInfo cinfo = img_c->QueryInfo(); colorBuffer = Mat(cinfo.height, cinfo.width, CV_8UC3); // copy data colorBuffer.data = data_c.planes[0]; colorBuffer = colorBuffer.clone(); // release access img_c->ReleaseAccess(&data_c); //img_c->Release(); } void RealSenseCVWrapper::getDepthBuffer() { Image *img_d = sample->depth; Image::ImageData data_d; img_d->AcquireAccess(Image::ACCESS_READ_WRITE, Image::PIXEL_FORMAT_DEPTH_F32, &data_d); Image::ImageInfo dinfo = img_d->QueryInfo(); depthBuffer = Mat(dinfo.height, dinfo.width, CV_32FC1); depthBuffer.data = data_d.planes[0]; depthBuffer = depthBuffer.clone(); img_d->ReleaseAccess(&data_d); //img_d->Release(); } void RealSenseCVWrapper::getMappedDepthBuffer() { // create projection stream to acquire mapped depth image Projection *projection = rsm->QueryCaptureManager()->QueryDevice()->CreateProjection(); Image *depth_mapped = projection->CreateDepthImageMappedToColor(sample->depth, sample->color); // acquire access to depth data Image::ImageData ddata_mapped; depth_mapped->AcquireAccess(Image::ACCESS_READ, Image::PIXEL_FORMAT_DEPTH_F32, &ddata_mapped); // copy to cv::Mat Image::ImageInfo dinfo = depth_mapped->QueryInfo(); depthBufferMapped = Mat(dinfo.height, dinfo.width, CV_32FC1); depthBufferMapped.data = ddata_mapped.planes[0]; depthBufferMapped = depthBufferMapped.clone(); // release access depth_mapped->ReleaseAccess(&ddata_mapped); depth_mapped->Release(); projection->Release(); } void RealSenseCVWrapper::getMappedColorBuffer() { // create projection stream to acquire mapped depth image Projection *projection = rsm->QueryCaptureManager()->QueryDevice()->CreateProjection(); Image *color_mapped = projection->CreateColorImageMappedToDepth(sample->depth, sample->color); // acquire access to depth data Image::ImageData cdata_mapped; color_mapped->AcquireAccess(Image::ACCESS_READ, Image::PIXEL_FORMAT_BGR, &cdata_mapped); // copy to cv::Mat Image::ImageInfo cinfo = color_mapped->QueryInfo(); colorBufferMapped = Mat(cinfo.height, cinfo.width, CV_8UC3); colorBufferMapped.data = cdata_mapped.planes[0]; colorBufferMapped = colorBufferMapped.clone(); // release access color_mapped->ReleaseAccess(&cdata_mapped); color_mapped->Release(); projection->Release(); } void RealSenseCVWrapper::getXYZBuffer() { Projection *projection = rsm->QueryCaptureManager()->QueryDevice()->CreateProjection(); std::vector<Point3DF32> vertices; vertices.resize(bufferSize.width * bufferSize.height); projection->QueryVertices(sample->depth, &vertices[0]); xyzBuffer.clear(); for (int i = 0; i < bufferSize.width*bufferSize.height; i++) { Point3f p; p.x = vertices[i].x; p.y = vertices[i].y; p.z = vertices[i].z; xyzBuffer.push_back(p); } projection->Release(); } void RealSenseCVWrapper::getColorBuffer(cv::Mat & color) { getColorBuffer(); color = colorBuffer.clone(); } void RealSenseCVWrapper::getDepthBuffer(cv::Mat & depth) { getDepthBuffer(); depth = depthBuffer.clone(); } void RealSenseCVWrapper::getMappedDepthBuffer(cv::Mat & mappedDepth) { getMappedDepthBuffer(); mappedDepth = depthBufferMapped.clone(); } void RealSenseCVWrapper::getMappedColorBuffer(cv::Mat & mappedColor) { getMappedColorBuffer(); mappedColor = colorBufferMapped.clone(); } void RealSenseCVWrapper::getXYZBuffer(std::vector<cv::Point3f> xyz) { getXYZBuffer(); xyz = xyzBuffer; } void RealSenseCVWrapper::useAutoAdjust(bool use_aa) { Device *device = rsm->QueryCaptureManager()->QueryDevice(); // get current values if you use manual mode device->SetColorAutoExposure(use_aa); device->SetColorAutoWhiteBalance(use_aa); } void RealSenseCVWrapper::setExposure(int32_t value) { rsm->QueryCaptureManager()->QueryDevice()->SetColorExposure(value); } void RealSenseCVWrapper::setWhiteBalance(int32_t value) { rsm->QueryCaptureManager()->QueryDevice()->SetColorWhiteBalance(value); } void RealSenseCVWrapper::getCalibrationStatus() { // aquire calibration data of RGB camera stream Projection * projection = rsm->QueryCaptureManager()->QueryDevice()->CreateProjection(); Calibration::StreamCalibration calib; Calibration::StreamTransform trans; projection->QueryCalibration() ->QueryStreamProjectionParameters(StreamType::STREAM_TYPE_COLOR, &calib, &trans); // copy RGB camera calibration data to OpenCV cameraMatrix = Mat::eye(3, 3, CV_32FC1); cameraMatrix.at<float>(0, 0) = calib.focalLength.x; cameraMatrix.at<float>(1, 1) = calib.focalLength.y; cameraMatrix.at<float>(0, 2) = calib.principalPoint.x; cameraMatrix.at<float>(1, 2) = calib.principalPoint.y; distCoeffs = Mat::zeros(5, 1, CV_32FC1); distCoeffs.at<float>(0) = calib.radialDistortion[0]; distCoeffs.at<float>(1) = calib.radialDistortion[1]; distCoeffs.at<float>(2) = calib.tangentialDistortion[0]; distCoeffs.at<float>(3) = calib.tangentialDistortion[1]; distCoeffs.at<float>(4) = calib.radialDistortion[2]; transform = Mat::eye(4, 4, CV_32FC1); for (int i = 0; i < 3; i++) { for (int j = 0; j < 3; j++) { transform.at<float>(i, j) = trans.rotation[i][j]; // todo: rotationの行と列の順を確認 } transform.at<float>(i, 3) = trans.translation[i]; } projection->Release(); }
cv::Matにおけるclone()とcopyTo()の挙動の違い
※本記事はOpenCV Advent Calender 2016向けに書きました。 http://qiita.com/advent-calendar/2016/opencv
OpenCVをちょっと知ってる人はこのタイトルで「何言ってんだこいつ」ってなったかも知れませんが，一見同じに見える（※後述）この2種類のdeep-copyメソッドは，実はある特定のコードで挙動が異なります．
その特定のコードとはROI処理です．StackOverflowでも「ROIへのコピーはcopyTo()を使えばできるよ！」と書いてありましたが，なぜ（自分が）普段から使うclone()を使わないのかについて言及する人がいなかったので，今回の検証に繋がりました．
ROIに画像を貼り付けられない!?
例えば画像処理で顔検出して，そこにアニメアイコンを貼り付けるような自動クソコラ生成器を作ろうとする場合，ROIを設定してそこに既存の画像を貼り付ける，なんてことをすると思います．しかし，それを素直にcv::Mat::clone()メソッドで実装しようとするとなぜか貼り付けられない場合があります．
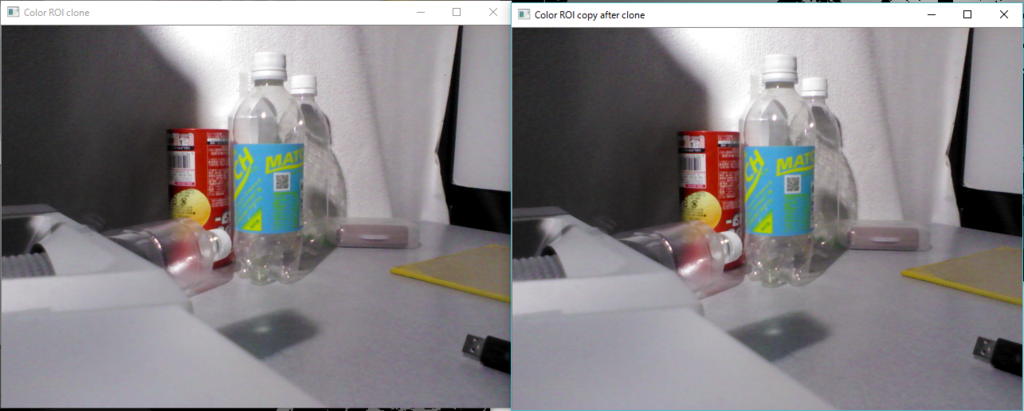
以下のコードは，次のような画像を作成しようとしているコードです．
// ROI Rect roi(100, 100, 100, 100); Mat img_roi = frame_c(roi); // 元画像のROIを生成 // clone Mat img_roi_clone = Mat(100, 100, CV_8UC3, Scalar(0, 255, 0)); // 貼り付ける画像を生成 img_roi = img_roi_clone.clone(); // 貼り付ける画像をcloneしてからROIに貼り付け imshow("Color ROI clone", frame_c); // なぜか貼り付けできてない
しかし，実際にこれで出てくる画像は・・・
このように，なぜか貼り付けできません．通常，ROIへの任意の画像処理は元画像frame_cに即座に反映されるため，このようにimg_roiに画像データをコピーすればROIの部分だけ塗りつぶされるはずなのですが，そうはならないようです．
そこでcv::Mat::clone()ではなくcv::Mat::copyTo()を使うと，目的の画像のようになります．
// ROI Rect roi(100, 100, 100, 100); Mat img_roi = frame_c(roi); // 元画像のROIを生成 // copyto Mat img_roi_copy = Mat(100, 100, CV_8UC3, Scalar(0,255,0)); img_roi_copy.copyTo(img_roi); // 貼り付ける画像をROIにコピー imshow("Color ROI copy", frame_c); // こうすると貼り付けできる
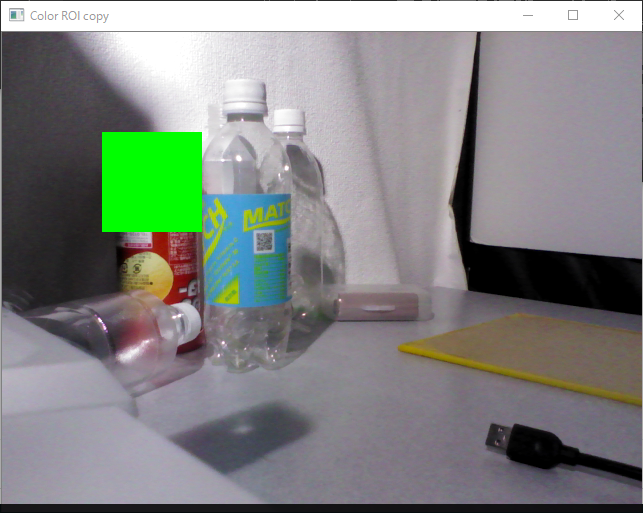
つまり，copyTo()でならROIに画像をコピーできるけど，clone()では画像をROIにコピーできないという仕様になっていることが確認できます．
※ちなみに，浅いコピー(shallow copy)img_roi = img_roi_shallow;は当然ながらうまくいきません．
やったね！今度からcopyTo()を使えばすべてうまくいくんだね！
更なる罠
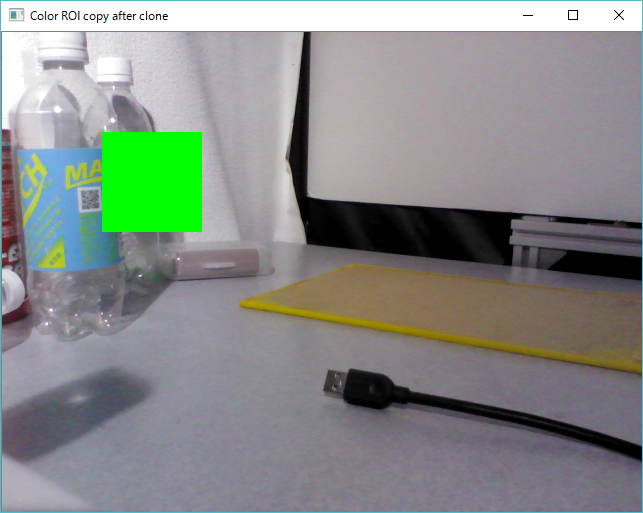
…って簡単にはいかないのが困りものです．実は，一度「うまくいかないコピー」でROIをコピーしようとしてしまうと，その後いくらcopyTo()で正しく書こうが一切反映されなくなります．
// ROI
Rect roi(100, 100, 100, 100);
Mat img_roi = frame_c(roi);
// clone
Mat img_roi_clone = Mat(100, 100, CV_8UC3, Scalar(0, 0, 255));
img_roi = img_roi_clone.clone();
imshow("Color ROI clone", frame_c); // これが反映されないのは知ってる
// copyto after clone
Mat img_roi_copy_clone = Mat(100, 100, CV_8UC3, Scalar(255, 0, 0));
img_roi_copy_clone.copyTo(img_roi);
imshow("Color ROI copy after clone", frame_c); // ナンデ！コピーできないナンデ！？
このソースコードによれば，clone()を使う方では赤い矩形が，copyTo()を使う方では先ほど描いた赤の矩形が青で塗りつぶされるため青い矩形がそれぞれ描かれるはずです．ただし我々は既にclone()が上手くいかないことを知っているので，clone()の時点ではframe_cに何も描かれず，copyTo()の方で青い矩形が初めて描かれるだろうと期待します．しかし，実際には
このように，どちらの画像にも全く矩形が描かれなくなります．勿論，clone()ではなく=を先に書いたとしてもうまく描かれなくなります．
clone()の仕様
clone()もcopyTo()も，行列cv::Matの「深いコピー(deep copy)」に分類されます．じゃあclone()とcopyTo()の何が違うんじゃい！って思ったプログラマの皆さんなら，OpenCVのソースコードを覗き込みたくなると思います．実際，cv::Mat::clone()がどんな実装なのか見てみましょう．
inline Mat Mat::clone() const { Mat m; copyTo(m); return m; }
......
...
同じやんけ！！！
どうやら内部的にcopyTo()を呼び出しているようです（リファレンスにもそう書いてありましたが，挙動が違うことを発見したので信じられなくなって確認しました）．しかしよく考えてみてください．clone()ではわざわざ自分自身をcopyTo()した画像を作って返しています．そういう意味で本当に自身のクローンを生成しているわけです．
原因の考察
ROIは通常の画像と同等に扱えるように見えるけれども，実際には元画像とデータを共有しているため，やはり普通のcv::Matとはちょっと違います．これらのことから，clone()では画像のクローンですべての情報が上書きされてしまい，元画像との参照関係が崩れてしまうのだろうと推察できます．浅いコピーの方でうまくいかない理由は，浅いコピーが実際にはデータポインタを上書きする（＝元の参照関係を外す）処理であるため，これもまた元画像への参照が失われてしまうことが原因と思われます．そう考えると，一旦関係が崩れてしまったROIにいくら正しい方法で上書きしても，元画像には影響しないことが容易に察せられます．
結論
今回は，ROI処理においてclone()，copyTo()およびoperator=(cv::Mat)の挙動に違いがあることを確かめました．結論としては，ROIが元画像とデータ共有している関係上，copyTo()以外を使うとその参照関係が崩れてしまい，それ以降の変更が反映されなくなるのが原因と推察できました．皆さんもROIを扱う時にはcopyTo()を使っていきましょう．
cv::Mat画像のサブピクセル画素値を取得
久々にOpenCVのTips
画像処理をしていると，テクセルサンプリングのように浮動小数点座標の画素値を取り出したい場合が時々出てきます．そういう時って普通，整数座標の画素値を使ってバイリニア補間するんですけど，なぜか OpenCVでは「特定の1点のサブピクセル画素を取得する」という処理を標準で用意していません（ちなみにcv::Mat::at<>()メソッドの座標値に浮動小数点数を入れてもコンパイルエラーは起きませんが，実際には暗黙的にintに変換された座標値からサンプルされます）．サブピクセル精度でコーナー座標を検出するcv::findCornerSubPix()みたいに画像からサブピクセル座標を割り出す処理はあるんですが，今回やりたいのはその逆なんです．
ただし，サブピクセル精度で画像を切り出す処理ならあり，cv::getRectSubPix()でできます．今回のTipsのアイディアは，これで得たいサブピクセル座標を画像中心として3x3画像で切り取り中央座標値をサンプルする，というものです．意外と気づかない手法だと思うので，書き残すことにしました．
// グレースケール画像mの要素をサブピクセル座標pから取得する // 通常のMat::at()メソッドでは四捨五入された座標から取得されてしまうのでcv::getRectSubPix()を利用する // 画像範囲外は境界線と同じとする // サポートする型はCV_32F or CV_8U double sampleSubPix(cv::Mat m, cv::Point2d p) { cv::Mat r; cv::getRectSubPix(m, cv::Size(3, 3), p, r); return (double)r.at<float>(1, 1); }
上のコードはグレースケール画像のみ対応ですが，同じ方法でカラー画像もできます．ただし，実はcv::getRectSubPix()はCV_8UもしくはCV_32Fにしか対応していない関数なので，要素がdoubleのCV_64F画像はサポートしていません．その場合は仕方ないので一旦castしましょう．
透視投影変換にガンマをかけて嘘パースを実現
はじめに
今回の手法で次のような絵が撮れます．
本記事ではフリーのMMD描画アプリを利用して嘘パースの実験をしていますが，シェーダーレベルでアプリを改造する上，原理のみ紹介するので，CGデザイナよりもむしろエフェクトを開発するプログラマ向けの記事となります．予め御了承下さいませ．
嘘パースについて
皆さん，嘘パース（オーバーパース，漫画パース）というのはご存知でしょうか？
例えば，サンライズアニメでよく見かける，例の武器を画面いっぱいに突き出して構える迫力ある構図（サンライズパース）をCGアニメで再現したいとします．しかし，実寸で作られたCGに同じポーズをさせて普通に透視投影変換でレンダリングすると，あんなに大きく武器が映りませんのでちょっと迫力に欠けてしまいます．なぜそんなことが起こるかというと，サンライズパースでは正確な透視投影よりも手前の物体がより大きく映るようにあえて強調した投影に従って描いているからです．このように，通常の透視投影変換ではありえないくらい近い物体が大きく写っているような投影を嘘パースと呼びます．アニメや漫画では迫力があった構図なのにCGにすると物足りない，という現象の原因は嘘パースだったりします．
現在，CGアニメで嘘パースを実現する方法は，その構図専用の歪んだCGモデルを用意する というのが一般的です．でも，それってかなり面倒くさいですよね．だって同じキャラクターなのに超カッコいい構図の度に新しいCGモデルを用意しなきゃいけないんですから．他には，自動で人物CGモデルを局所的に肥大化させる手法（嘘パースプラグイン），画角の異なるカメラを複数用意してシームレスに映像を合成して実現する手法（マンガパース）などが知られています．
ここでは，より原理的な部分に着目して嘘パースを実現する手法を考案しました．それが，透視投影変換にガンマをかける という発想です．ディスプレイガンマのようにZ軸方向にガンマをかけることで，人間の知覚に近い歪み方をとっても簡単に再現できるのではないか？と思って試してみました．これは新しい投影変換を開発する必要がありますので，ちょっと考え方を示していきます．
原理
通常の透視投影
デザイン系の人には遠近法と言った方がわかりやすいかもしれないですが，透視投影とはすべての光線がある唯一の視点（原点）に集中するものとして考案された投影法です．
透視投影をCGで実現するには，レンダリング時に透視投影行列という同次変換行列（下式）をかませます．これによって，透視投影の視錐体がクリッピング空間に圧縮されるわけです．
透視投影にガンマをかける
透視投影では，物体の見た目の大きさは視点からの距離に反比例するという性質があります．3DCGプログラマにとっては非常に当たり前のことに思えますが，それはなぜでしょう？理由は，透視投影では光線が原点に直線的に集まると仮定しているからです．もちろん，この仮定は物理的には間違ってません．
対して嘘パースでは，視点の物体が通常の透視投影よりも極端に大きくなるという性質があります．透視投影では直線 に従って投影面
での見た目の大きさを決定していましたが，私はここでガンマ変換をかけることにしました．つまり，人が奥行きのあるシーンを観察したときに，スティーブンスの冪乘則に従って奥行知覚が実際の奥行きよりも強調される と仮定しました（これが事実かどうかは私は知りません）．この時の投影は次のようになります．
このようにすると，同じ大きさの物体でも遠くにあれば投影面ではより小さく映り，逆に近い物体はより大きく映ることになります．具体的には，同じ物体の見た目の大きさはの逆数に比例します．
ガンマ透視投影変換
この考えに基づいて投影行列を再構成すると，次のようになります．ここではガンマ透視投影変換と呼ぶことにします．とすると元の透視投影行列と一致するはずです．プログラム的には，モデルビュー行列をかけた後に一旦Z軸を編集する必要があるのでちょっと面倒ですが，バーテックスシェーダーで難なく実装できるでしょう．
実験
今回はMMD on WebGLのソースコードを改変して，初音ミクの標準モデル（あにまさ式）で試してみました．この場を借りて作者様に感謝します．
結果
まずは通常の透視投影変換でレンダリングした結果がこちらです．
これとほぼ同じ構図，ポーズで でガンマ透視投影変換でレンダリングした結果が次のようになります．
狙い通り，前方に突き出した手がかなり強調される嘘パースが実現できました．
今回の目的とは異なりますが，逆に とガンマを1より小さくした場合どうなるかというと...
こうなります．奥の方の手が透視投影よりも大きく映ります．偶然かもしれませんが，平行投影に似ています．
注意点
上の結果はかなりうまくいってるようですが，実はガンマ透視投影では構図をうまく調節しないとすぐにひどい結果になります．
このように，画面の外側は激しく歪みやすいです．しかし改善策はあります．ガンマ透視投影行列の光軸中心（行列の3列目の上２個）をずらしてやることで，ある程度問題を回避できるようです．
上２つはほぼ同じ方向からほぼ同じポーズをレンダリングしたもので，上は光軸中心を中央に固定しており，下では光軸中心を顔付近に持ってきています．このように，光軸を中央からずらして調節することで，ほぼ違和感のない嘘パースが様々な構図で実現できるようです．
経験則ですが，初音ミクのような人体モデルの場合はガンマによって頭部が歪むと強く違和感を覚えるので，頭部だけは歪まないように構図を調節すると良いでしょう．
倒立振子制作日記（そのに）
PWMによる電流制御
前回の記事でも取り上げましたが，この記事によるとDCモータで出力制御系を構成するときは電圧入力ではなく電流入力にすると理論的扱いがしやすいとのことですので，私もこの記事と同様に電流入力系を構成しようと思います．（注：以下，超基本的な所から説明します）
ちょっと復習
DCモータにはT-I特性（トルクvs電流）とT-N特性（トルクvs回転数）というものがあり，トルクと電流は比例し，負荷トルクが増すと直線的に回転数が減少する，という特性があります（ちなみに電圧を変えるとT-N特性が平行移動します）．つまり電流入力さえできればその時の負荷トルクさえ分かれば回転数（速度）が制御できることになります．
で，どーすんの？
さて一方で，例えDAコンバータを積んでいたとしてもマイコンにできるのはGPIOの電圧出力を変調することのみです．更に言うとArduinoUNOにはDACもないのでPWM出力をアナログ出力とみなすしかありません．モータの自己インダクタンスとか慣性とか非線形摩擦とかを考慮して，Hブリッジへの入力電圧だけでモータ入力電流値を予測するのは困難です．
そこで出てくるのが電流フィードバックです．これはモータへの入力電流を何らかの方法で計測し，その測定値をPWM出力にフィードバックして目標電流値を実現する，というものです．今回使用したモータドライバL298Nにはセンサ用PIN（と称するHブリッジの下流）がありますので，抵抗を挟んでGNDに接続し，抵抗間の電圧をアナログ入力に読ませることにしました．以前の記事では電流計測ICを用意していましたが，使い方が悪いのかセンサ自体の性能かわかりませんがノイズでかすぎて使い物にならなかったので抵抗にしました．
64種類 各20個（合計1280個）金属膜抵抗キット 1/4W（0.25W） 許容差±1%
- 出版社/メーカー: Ecowsera
- メディア: エレクトロニクス
- この商品を含むブログを見る
この抵抗セットがめちゃくちゃ便利でした．そんなに大量に使う予定がないなら，アキバでバラ100本入り100円とかで買うより良いかも．
コーディングする前に
電流センサ抵抗の選定
電流センサ抵抗の値はどうすればいいのか．これは中学生でも知っているオームの法則を利用します．下に今回の電流計測回路の簡単な回路図を示します．
Vss
|
[M] Motor (実際はHブリッジで接続)
|
|---- V (Analog Input)
|
I >
↓ > R
>
|
|
---
///
マイコンのアナログ入力はハイインピーダンスであるため，Analog Inputへは殆ど電流が流れません．そのためモータ入力電流は抵抗電流 \(I\) で近似でき，オームの法則 \(V=RI\) を利用してモータ入力電流をアナログ入力から得ることができます．従って，Analog Inputの許容最大電圧とMotor入力として想定する最大入力電流が分かれば \(R\) の値を見積もれます．
ArduinoUno(互換機)のアナログ入力の許容最大電圧はマイコン電源電圧と同じ \(V_{cc}=5[V]\) であり，モータドライバL298Nの定格最大電流は \(I_{max} = 2[A]\) であるので，
\(R = V_{cc} / I_{max} = 5[V]/2[A] = 2.5[\Omega]\)
と求められます．しかし現実には電池の供給能力の関係上2[A]も出せませんし，消費電力を考えると抵抗は小さい方がモータ入力に割く電流が大きくとれ，制御に有利そうです．そこで抵抗値をもっと下げて \(R=1[\Omega]\) にしてみるとどうでしょう．すると，定格最大電流は変わらないので想定最大電圧は
\(V_{max} = RI_{max} = 1[\Omega] \times 2[A] = 2[V]\)
と，先程の5[V]よりだいぶ低くなってしまいました．マイコンのアナログ入力の最大値は変わらず5[V]ですので，これはセンサ入力の分解能が低下することを意味します．計算は省略しますが，逆に抵抗値を増大させてセンサの分解能を上げようとする場合，そもそもの制御量であるモータ入力電流の最大値が減少してしまいます（或いは，最悪の場合マイコンのアナログ入力回路を破壊する程の電圧を許容することになります）．ということでここはバランスよく決めなくてはなりません．今回は手元に2.2[Ω]の抵抗があったので，最初の計算に近いということもありこいつを使います．
アナログ入力から電流値への変換
電子工作やPCに疎い人は分からないかもしれないので一応説明しておくと，実はマイコンのアナログ入力から直接返ってくる値は物理的な電圧値（実数）ではなく，それをADコンバータ(ADC)が読み取ってADCの精度(bit数)に応じて予め決められた最大値との比を整数値で返す，という動作をします．例えば，5[V]駆動の8bitADCに2[V]を入力すると，
\(256 \times {2[V] \over 5[V]} = 102.4 \simeq 102\)
という値が返ってきます．従ってこの逆算式
\(V = V_{max} \times {A \over A_{max}}\)
を通して物理値である電圧が得られますね（AはADCの出力）．更にセンサ値（今回は電流値）に変換するには電圧とセンシングしたい値との関係式をデータシートから読み取って実装すればいい訳です．今回はその関係式とはオームの法則に他ならないので， \(I=V/R\) として先程選定した抵抗値をぶち込めば晴れて電流値を読み取ることができます．
フィードバック制御
今回は速度型PI制御器を構成しました．同じPID制御でも位置型と速度型があるようで，位置型は制御量uそのものをPIDにより求めるもの，速度型は制御量uの増分をPIDにより求めるものです．今回の場合は電圧で直接電流を制御するので，以前の電流入力を保持する構造が何もありません．従って位置型にすると目標値に達した瞬間に電圧が0になり電流が急低下するといった現象が起こると考えられるので，速度型を採用する方が良さそうです．電流もいわば速度だし．
というわけで，制御量の数式は以下のようになります．
\(
u_t = u_{t-1} + \Delta u, \)
\(\Delta u = K_pe_t + K_i\sum_t{e_t},\)
\(\space e_t = I_\theta -I_t
\)
フィードバックゲインは限界感度法っぽい感じで適当に決めました．
制御量のPWM出力への変換
制御量をどうやってPWM出力に変換するのかも悩みどころです．制御量uは電流から生成したので，duty比が最大になった時に想定した最大電流が流れると仮定して，次の変換式に掛けました．
\(duty \space cycle = 255 \times {u_t/I_{max}}\)
255というのはArduinoのPWM出力が8bitだからです．単位がごちゃごちゃだし，あとあと考えてみると変な仮定な気がしますが，電流を電圧にしたところでゲインが変わるだけだし，これで動いたのでとりあえず良しとしましょう．
Arduinoスケッチ
CurrentFeedback.h
#ifndef CURRENTFEEDBACK_H_ #define CURRENTFEEDBACK_H_ #include "Arduino.h" #define LOOP_MAX 20 // アナログ入力平均化ループの周期 #define ANALOG_MAX 1024 // アナログ入力は10bit #define DUTY_MAX 255 // デューティ比は8bit // 定数 // current_max = analog_voltage / current_resist = 2.27A const float analog_voltage = 5.0; // アナログ最大電圧[V](analog = 1024) const float current_resist = 2.2; // モータ電流抵抗[ohm] const float current_max = 2.27; // モータ印加電流最大値[A] class CurrentFeedback{ protected: // Pin int analog_pin; // 電流センサ int input1_pin; // 正回転 int input2_pin; // 逆回転 int enable_pin; // PWM出力 // 内部変数 float current_target; // モータ印加電流の目標値[A] float Kp_current; // 電流比例フィードバックゲイン float Ki_current; // 電流積分フィードバックゲイン float error_integral; // 誤差積分値 float pwm_duty; // PWM出力のデューティ比（-255.0 ~ 255.0） public: // コンストラクタ CurrentFeedback(){ } CurrentFeedback(int analog, int input1, int input2, int enable, float feedback_gain_p = 1.0, float feedback_gain_i = 1.0){ begin(analog, input1, input2, enable, feedback_gain_p, feedback_gain_i); } // デストラクタ ~CurrentFeedback(){ } // 初期化関数(PIN, フィードバックゲインの登録) void begin(int analog, int input1, int input2, int enable, float feedback_gain_p = 1.0, float feedback_gain_i = 1.0){ // 引数の保存 analog_pin = analog; input1_pin = input1; input2_pin = input2; enable_pin = enable; Kp_current = feedback_gain_p; Ki_current = feedback_gain_i; // 値の初期化 current_target = 0; pwm_duty = 0; error_integral = 0; } // 目標値の登録 void setTargetCurrent(float target_current){ current_target = target_current; } // 現在の測定値を読みだす float getCurrent(){ // ADCの平均出力値を算出 float analog_mean = 0; for(int i=0;i<LOOP_MAX;i++){ int a = analogRead(analog_pin); analog_mean += (float)a/LOOP_MAX; } // ADC出力値から電流値への変換 float current_sense = analog_mean / ANALOG_MAX * analog_voltage / current_resist; current_sense = (digitalRead(input1_pin) == HIGH)? current_sense : -current_sense; // 印加電流の符号を決定 return current_sense; } // 登録した目標値に向けてフィードバック制御 void output(){ // sensor float current_sense = getCurrent(); // モータ印加電流の実測値[A] 符号は回転方向 // controller // フィードバックコントローラ 速度型PI制御 float current_error = current_target - current_sense; // 誤差 error_integral += current_error; float control_input = Kp_current * current_error + Ki_current * error_integral; // PI制御 pwm_duty += control_input / current_max * DUTY_MAX; // current -> duty cycle(-256 ~ 255) if(pwm_duty > DUTY_MAX) pwm_duty = DUTY_MAX; else if(pwm_duty < -DUTY_MAX) pwm_duty = -DUTY_MAX; int pwm_dst = (int)abs(pwm_duty); // actuator // モーター回転方向 if(pwm_duty > 0) { digitalWrite(input1_pin, HIGH); digitalWrite(input2_pin, LOW); } else if(pwm_duty < 0) { digitalWrite(input1_pin, LOW); digitalWrite(input2_pin, HIGH); } else{ digitalWrite(input1_pin, LOW); digitalWrite(input2_pin, LOW); } analogWrite(enable_pin, pwm_dst); } // 緊急停止 void quickStop(){ current_target = 0; pwm_duty = 0; digitalWrite(input1_pin, HIGH); digitalWrite(input2_pin, HIGH); analogWrite(enable_pin, 255); } }; #endif // CURRENTFEEDBACK_H_
こんな感じでクラス化してみました．Arduino IDEでクラスを書くのは初めてだし，ArduinoでC++記法がどこまで許されてるのか分からなかったのでちょっと大変でしたが，なんとかうまくいきました．やっぱC言語よりクラスが書けるC++の方が慣れると便利ですね．
動作テスト用スケッチ
#include "CurrentFeedback.h" #define MOTOR1_INPUT1_PIN 4 // Input 1 #define MOTOR1_INPUT2_PIN 5 // Input 2 #define MOTOR1_PWM_PIN 6 // Enable 1 #define MOTOR1_CURRENT_PIN 1 // Analog 1 CurrentFeedback current1; float current_target = 0; void setup() { // put your setup code here, to run once: Serial.begin(19200); Serial.println("hello"); current1.begin(MOTOR1_CURRENT_PIN, MOTOR1_INPUT1_PIN, MOTOR1_INPUT2_PIN, MOTOR1_PWM_PIN, 1.2, 0.4); } void loop() { // put your main code here, to run repeatedly: // シリアル入力（目標値の決定） char c = Serial.read(); if(c == '1'){ if(current_target > -current_max){ current_target -= 0.05; } else{ current_target = -current_max; } Serial.println(current_target, DEC); } if(c == '2'){ if(current_target < current_max){ current_target += 0.05; } else { current_target = current_max; } Serial.println(current_target, DEC); } if(c == '3'){ current_target = 0; Serial.println(current_target, DEC); } if(c == '4'){ current_target = 0; current1.quickStop(); Serial.println("------------STOP------------"); } current1.setTargetCurrent(current_target); current1.output(); Serial.print(" "); Serial.println(current1.getCurrent(), DEC); }
シリアルモニタからモータの入力電流を指定してそのときの測定値を出力させるプログラムです．実行した結果は，ハンチングが激しいですが電流値は一応制御できてるっぽいです．やったぜ．
（2016/09/19修正）ADCとDACを書き間違えていたので修正