すっごくわかりにくい「明るさ」のはなし 〜Aqoursを添えて〜
だいぶご無沙汰していましたが,今回は私の専門の一つである色彩科学に関する話をしたいと思います.今回は明るさ,あるいは明暗,あるいは光の量を表す単位について,測光学の観点からできるだけ正確に書くことを試みます.
以下の文章は私が自分の知識の整理のために書くものです.よって厳密な正確性は保証しません(大学のレポートで使って×をつけられても知らないゾ!).まだ不勉強な部分も多々ありますので,もし違っていたらご指摘お願いします.
あと,おたく特有の表現が出てきます.
(20211021追記:重さ対策のため,数式を行形式表示にしました.)
その前に
光の明るさや明暗を表す用語は様々で,それぞれに微妙な違いがあります.例えば「輝度(luminance)」「照度(illuminance)」「明度(lightness)」「明るさ(brightness)」というのはそれぞれ明暗の違いを表す専門用語ですが,厳密にはこれらは全て違う概念です.以下ではこの違いについても詳しく触れていきます.従ってここでは,一般的な意味での明るさという表現を「明暗」と呼ぶことにします.
前提知識としては,電磁波の強度がエネルギー[W]で表せることを知っておけばいいでしょう.
明暗を定量的に取り扱うには
明暗は何から生じるでしょうか?光ですよね.光とは何でしょうか?電磁波です.では電磁波の強さを物理的に定量化すれば明暗の強さを定義できそうな気がしますよね?

ぶっぶー!ですわ!
これがやりたかった
考えてみてください.X線がいくら強かろうが,赤外線がいくら放射されてようが,携帯から無線の電波がいくら屋内を飛び回っていようが,明暗感覚には全く影響しません.ヒトが眼で感じられる光の範囲は決まっていて,およそ380nm~780nmの波長範囲の電磁波です.この範囲の光のことを「可視光」と呼びます.
「わかった!じゃあ可視光範囲だけ考えることにしよう!」
「悪くありませんわね.」
「確か光には線型性があるから,積分で表せる...だったよね?」
「その通りですわ!千歌さんにしては賢いですわね.」
「可視光範囲の単位時間あたりの放射エネルギー密度I [W/m^2],なんて...どうかな?」
「式にすると?」
「E(\lambda)をその光の波長\lambdaにおける放射エネルギー密度分布[ W/(m^2 \lambda) ]として...こうだ!」
I =\int_{380nm}^{780nm} E(\lambda) d\lambda

ぶっぶー!ですわ!
千歌ちゃんがなぜ怒られたのかというと,波長(色)による明暗の違いを全く考慮に入れてないからです.可視光の単色光,かつ同じ放射エネルギー密度であっても,ヒトにとっての明暗の感じられ方は大きく異なります.直感的にも,一般に青は暗くて黄色は明るく見える,というのは納得ですよね(この説明はちょっと厳密性に欠けますが).これを表したのが分光視感効率と呼ばれるものです.((2018/2/20追記)以降,単に「光」といった場合,分光視感効率を考慮した可視光を意味します.)
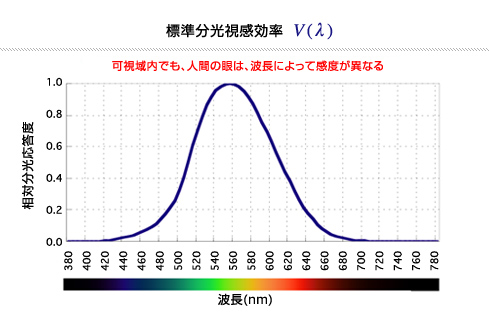
このグラフは,物理的に同じエネルギーを持った単色光が,ある波長の時にどれだけの明暗量(正確には輝度)としてヒトに知覚されるかを相対的に表したものです.例えばこのグラフから,480nmの単色光は560nmの単色光よりも約0.1倍明るく見える(=10倍暗く見える),ということが読み取れます.
ちなみに分光視感効率をどうやって測定するかというと,フリッカーフォトメトリー(Flicker Photometry,交照法)と呼ばれる心理物理実験を使います.被験者に2種類の単色光をチカチカと素早く点滅させた光(フリッカー)を見せて「チラつきが見えなくなるように」一方の単色光の強度を調節してもらいます.チラつきは明暗に差があるときに生じると考えられるため,チラつきが無い=明暗に差が無いと考えることで,相対的な明暗感覚の効率を波長分布として求めることができます.
ここまでで大事なことは,明暗量は物理量だけでなくヒトの心理特性まで考慮しないと定義できない量(心理物理量)であるということです.明暗を表す単位の一つ「カンデラ[cd]」が,SI基本単位の中で唯一,物理的に定義されていないのはこれが理由です.
※実は音の心理的な大きさを表すラウドネス[phon]も心理物理量であり,物理的に同じ音圧[Pa]であっても周波数毎に異なる量です.が,なぜかこちらは基本SI単位には含まれてません.
様々な明暗量の定義
輝度(Luminance)
上記の分光視感効率を用いて定義した,ある一点における明暗の量のことを「輝度」と呼びます.単位はカンデラ毎平方メートル[cd/m^2]あるいはニト[nt]で,計算式は次の通りです.
L=683\int_{380nm}^{780nm} E(\lambda) V(\lambda) d\lambda
このように輝度は積分で定義されるため,線型性が成り立ちます.これはつまり,異なる分光分布を持つ光源でさえも,輝度に対しては足し算や平均をしてよいことを意味します.
輝度は一般に,発光面(例えばディスプレイモニタ)の局所的な明暗を表す量として広く使われています.例えば,一般的なPCモニタの白色(255,255,255)は大体数百cd/m^2です.
ちなみに,たまに輝度のことをBrightnessという人たちもいますが,測光学的には厳密には間違いです.
※訂正(2018/2/20):輝度の単位を間違えていたので修正.
光度(Luminous intensity)
さて,輝度の単位を見ると/m^2とついていますので,面積で積分してみたくなりますよね?すると,ある大きさを持った面光源,あるいは完全拡散反射面全体としての明暗量を与えることになります.これを「光度」と呼びます.単位はカンデラ[cd]です.光度はある方向から見た面全体としての明暗を表す量なので,例えば面を傾けて見た場合,輝度は減りませんが光度は減ります.光度は一般に,光源の面積を考える意味のないもの(例えば星)の明暗を表す時に使います.点みたいな星の見かけの面積で微分したら無限大の輝度になるし.
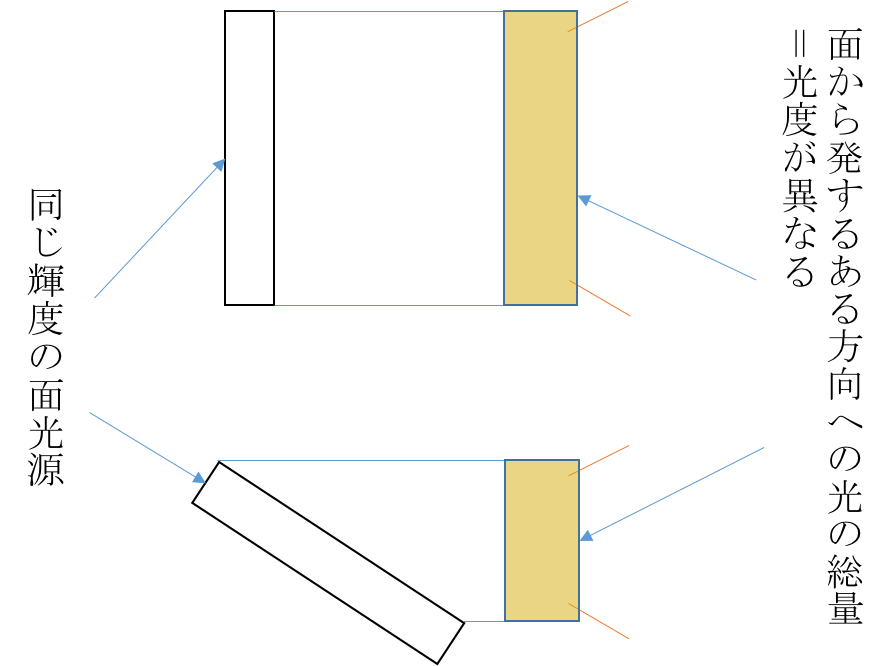
ちなみに,一般的なロウソクの火はおよそ1cdです.これは元々,光度の単位の定義にロウソクの火を用いていたことと関係します.
光束(Luminous flux)
光束という言葉は聞いたことがなくても,その単位「ルーメン[lm] = [cd str]」というのは,照明を買う時に気にしたことがあるかもしれません.光束とは,点光源から発生する,明暗を決める光の量そのものを表す量です.
「...ということですのよ!皆さん,分かりましたか?」
「いやぁ...だって光の量は光度ってさっき言ってなかったっけ?」
「光束と光度で何が違うの?ダイヤの言ってること良く分かりマセーン!」
「えっ...と...それは...」

では例えば,2種類の配光特性の異なる点光源を考えてみましょう.これらを同じ面積の孔から覗いてみます.
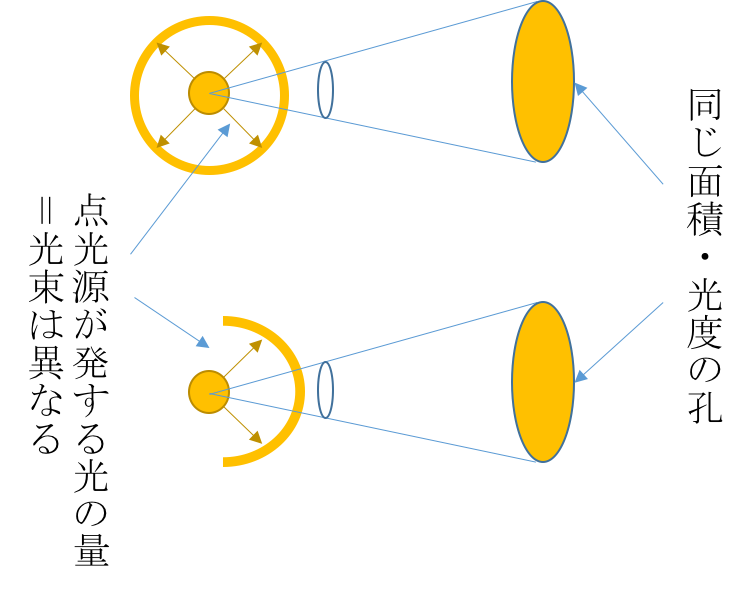
このとき,孔の光度(面全体で均一ならば輝度)が等しかったとします.しかし,光源A(上)はあらゆる方向に光を発する一方で,光源B(下)はある方向にしか光を出しません.孔を通過する光の量は確かに同じと言えますが,光源Aと光源Bは果たして全体として同じ量の光を放射していると言えるでしょうか?このような光の量の違いを表すのが,光束という量です.
点光源からは3次元的にあらゆる方向へ光が発せられるので,光束を計算するには2次元的な角度ではなく立体角で考えます.ですので,点光源から発せられるある面積Sを通過する光束\Phi(S)は,Sが張る立体角\omega(S)の積分として定義されます.
\Phi(S) = \int_{\omega(S)} I d\omega
逆に言えば,光度は光束の立体角密度とも言えます.つまり,同じ光束の光源であっても鏡などで指向性を持たせてやれば,その方向においては光束の密度すなわち光度が大きくなります.懐中電灯とか豆電球のくせにやけに明るいですよね.
ちなみに\omega=4\pi,つまり点光源を囲む球面を考えた場合の光束のことを全光束と呼びます.全光束は点光源からあらゆる方向に発せられる光全てをカウントした量ですので,光源そのものの発光能力を示しているといえます.これが照明の能力を示す指標として全光束[lm]が使われる理由です.
照度(Illuminance)
一方で,光源や面で反射する光ではなく,光に照らされている対象の立場で考えた時の明暗を表す量も考えるべきです.同じ全光束の光源で照らしていても,その光源があまりにも遠い場所では暗いですよね.そのような明暗を表す量が照度で,単位はルクス[lx]=[lm/m^2]です.
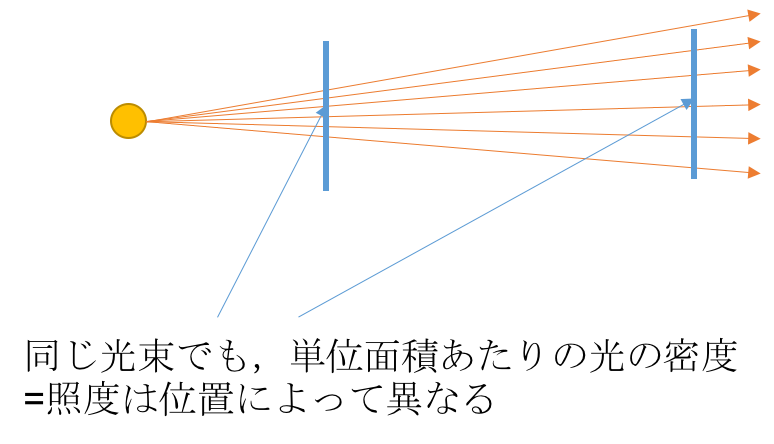
電気力線と同じく,光束は光線として考えることができます.点光源から離れれば離れるほど,同じ面積を通過する光線の数は減っていきます.これが照らされた時の明暗すなわち照度に相当します.従って定義式は次のようになります:
E={d\Phi \over dS}
「うぇ,またなんか変な式が出てきたぁ!はっ,これぞもしや光と闇の魔術の真髄…!」
「いや,ある意味間違ってないけどむしろ初歩だから...」
「リリーには解ってしまうのね...この魔界から誘わんとする冥府の囁きが...」
「違うから!っていうか,光度や輝度と照度って何が違うのかしら?」

ある方向から出て行く単位立体角あたりの光線数(光束)が光度です.立体角は距離によって変わりませんので,光源から遠ざけてもその方向の光度は変わりません.一方で照度は単位面積あたりの光線数(光束)ですので,上で書いたように照度は光源から遠ざけると小さくなります.
均一な面光源の場合には輝度を考えます.この場合,光源の輝度は距離によって変化しません.しかし,このような面光源で照らした時の照度は光源からの距離によって変わり,照らされた面の反射光の輝度もまた変化します.実は,照らされている面の照度と,その面の反射光の輝度には次の関係式が成立します.
L={\rho \over \pi} E
ここで\rhoは面の反射率です.証明は簡単なので飛ばします.このように,照度は反射面上に降り注ぐ光の明暗を表し,輝度は発光面あるいは反射面を見る時の明暗を表します.ここら辺,かなり分かりにくいと思いますが,よく読むと分かるはずです.
(2018/2/20追記)ちなみに,一般的なオフィスの照明設置条件では500~1000lxくらい,曇りの日の外だと数万lx,直射日光下だと大体10万lxくらいあります.太陽って凄まじい照度ですね.まぁ,真に凄いのはそんな幅広い照度範囲でも正常に機能する人間の眼の順応能力なのかも知れませんが....
輝度は「明るさ」なのか?
さて,ここからは反射面の明暗のみについて議論していきます.これまで紹介した中で使えそうな用語は「輝度」ですが,果たして輝度は直感的な意味での「明るさ」と本当に対応しているのでしょうか?
例えばスマートフォン.明るさ調節機能を切った場合にはスマホの輝度は一定に保たれるはずです.この状態では勿論,まともに使えませんよね.屋外に出れば画面が暗すぎるし,寝る前に電気を消して画面を見ると明るすぎる,なんてことになります.つまり我々は,直感的な意味で「面の明るさ」と言った場合に,無意識的にその空間から見た相対的な明暗を判断しています.
また一方で,明るさ知覚量は輝度に比例しないことが知られています.すなわち,100[cd/m^2]と200[cd/m^2]の差と,1000[cd/m^2]と1100[cd/m^2]の差は同じ明るさの差ではないのです.このことからも,輝度をそのまま明るさの単位とすることはできなさそう,ということがわかります.
「うーん…確かにスマホの明るさは違うね…」
「輝度と明るさが違うとなると,明るさってなんだろう?数値化できるのかな?」
「難しい問題ですわね…」

明度(Lightness)
少なくとも物体表面の明暗知覚については,ある程度数値化が試みられています.それはメイド明度と呼ばれています.計算式は以下の通り.
L^* = 116(Y/Y_n)^{1/3}-16 (if Y/Y_n \geq (6/29)^3)
L^* = 903.29 Y/Y_n (othewise)
ここでYは物体表面の反射光の輝度,Y_nはその環境下における完全拡散反射面(=白色点,白色標準)の輝度を表します.上式から明度は,その環境下で反射面としてありうる最大輝度で正規化した反射光輝度の非線形出力として与えられることがわかります.これによって上で述べた「明るさの相対評価という特性」「輝度と明るさの非線形性」の2点をクリアしています.正規化しているため単位はありませんが,0~100の値をとるので,強いていうなら%でしょうか.
これはマンセル表色系という,色票の色を明度・色相・彩度の3要素で表現し,かつ知覚的に等間隔になるように定量的に表した表色系をもとに構成(近似)されています.マンセル値は色票固有の値なので,明度も色票固有です.上式で得られる明度は,反射面が定まれば照明によらず一意に定まります.
明るさ(Brightness)
物体表面に限って言えば,明るさはほぼ明度と対応します.ただし,明度と明るさは厳密には異なります.
「…って本に書いてあったずら.」
「お姉ちゃん,これって一体どういう事なの?」
「さあ,洗いざらい吐いてもらうわよっ!」
「ピギャアアアアアアアア!!知りませんわあああああ!!」

明度は物体表面に関する明暗知覚を表すので,厳密には発光面に対しては適用できません(ただしモニタの最大輝度を白色点として,擬似的に明度を求めることはできます).対して明るさは,表面以外にも定義されうる量です.しかし,CIE(国際照明委員会)で「明るさ(brightness)」を表す心理物理量は現状採択されていません(2018/2/20追記:輝度とBrightnessの関係を測定している論文はありますが,有彩色光まで含めて明るさの関数を求めた例は私は知りません).
他にも,照度を大きくすると,(表面自体が変わるわけではないので)明度は変わりませんが,明るさは変化します.相対的な量としても,白はより明るく(明度が高くなったように),黒はより暗く(明度が低くなったように)見えるようになります(スティーブンス効果).また,明度の式からいえば,同じ照度下で同じ輝度ならば同じ明度になります.しかし実際には,そのような条件下で彩度の異なる色光・色票を観察した場合,高彩度の方がより明るく見えることが知られています(ヘルムホルツ-コールラウシュ効果).更に最新の研究では,錐体の応答量だけでは明るさ知覚を説明できず,別の視細胞も関わっているのでは,なんて話も浮上しつつあります.
以上のように,「明るさ」と一言で言っても,そこには絶対的な明るさ(輝度と対応)と相対的な明るさ(明度と対応)が混在しています.そしてそのどちらについても,明るさを正確に表す式は今の所存在しません.実は明るさ知覚については今のところまだ解っていないことが多く,皆が納得できる形で定量化しきれていないのが現状です.
まとめ
ここまでに,心理物理量としての輝度,光度,光束,照度の定義,考え方と,それらの違いを説明しました.更に,輝度,明度,明るさは似た概念でありながら互いに完全には一致しないことを解説しました.特に明るさについては,現在は未だ完全な数値化ができていない量であることを述べました.
「…というわけで,明るさの話はこれでおしまいです.ルビィ,わかりましたか?」
「うん,複雑な話だったけどお姉ちゃんのお陰でよく分かったよ!」
「んまああああ!!流石私の妹!かわいいでちゅね〜よくできまちた〜」

「何これ…」
「さぁ…」
「明るさの話だけに2人共シャイニー☆ってことね!」

お粗末.